
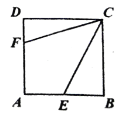
【題目】如圖,正方形![]() 的邊長為12,點
的邊長為12,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,若
上,若![]() ,且
,且![]() ,則
,則![]() ______.
______.
【答案】![]()
【解析】
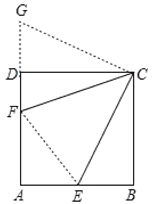
首先延長FD到G,使DG=BE,利用正方形的性質得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性質易證△GCF≌△ECF,利用勾股定理可得DF,求出AF,設BE=x,利用GF=EF,解得x,再利用勾股定理可得CE.
解:如圖,延長FD到G,使DG=BE;
連接CG、EF;
∵四邊形ABCD為正方形,
在△BCE與△DCG中,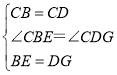 ,
,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF與△ECF中,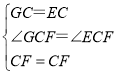 ,
,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵DF=![]() ,AB=AD=12,
,AB=AD=12,
∴AF=124=8,
設BE=x,則AE=12x,EF=GF=4+x,
在Rt△AEF中,由勾股定理得:(12x)2+82=(4+x)2,
解得:x=6,
∴BE=6,
∴CE=![]() ,
,
故答案為:![]() .
.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,直線CD與⊙O相切于點C,且與AB的延長線交于點E.點C是弧BF的中點.
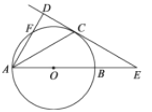
(1)求證:AD⊥CD;
(2)若∠CAD=30°.⊙O的半徑為3,一只螞蟻從點B出發,沿著BE--EC--弧CB爬回至點B,求螞蟻爬過的路程(π≈3.14,![]() ≈1.73,結果保留一位小數.)
≈1.73,結果保留一位小數.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為﹣6,點B在數軸上A點右側,且AB=14,動點M從點A出發,以每秒5個單位長度的速度沿數軸向右勻速運動,設運動時間為t(t>0)秒.
![]()
(1)寫出數軸上點B表示的數 ,點M表示的數 (用含t的式子表示);
(2)動點N從點B出發,以每秒3個單位長度的速度沿數軸向右勻速運動,若點M,N同時出發,問點M運動多少秒時追上點N?
(3)若P為AM的中點,F為MB的中點,點M在運動過程中,線段PF的長度是否發生變化?若變化,請說明理由;若不變,請求出線段PF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算.
(1)(﹣3)×(+4)﹣48÷|﹣6|
(2)77°53'26″+33.3°(結果用度分秒形式表示)
(3)[﹣14﹣(1﹣0.5×![]() )]×[3﹣(﹣3)2]
)]×[3﹣(﹣3)2]
查看答案和解析>>
科目:初中數學 來源: 題型:
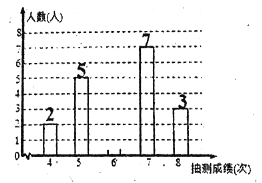
【題目】為了解某校八年級男生的體能情況,體育老師從中隨機抽取部分男生進行引體向上測試,并對成績進行了統計,繪制成兩個不完整的統計圖,請結合圖中信息回答下列問題:
(1)本次抽測的男生有 人,請將條形圖補充完成,本次抽測成績的中位數是 次;
(2)若規定引體向上6次及其以上為體能達標,則該校500名八年級男生中估計有多少人體能達標?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于實數a,b,我們可以用min{a,b}表示a,b兩數中較小的數,例如min{3,-1}=-1,min{2,2}=2. 類似地,若函數y1、y2都是x的函數,則y=min{y1, y2}表示函數y1和y2的“取小函數”.
(1)設y1=x,y2=![]() ,則函數y=min{x,
,則函數y=min{x, ![]() }的圖像應該是 中的實線部分.
}的圖像應該是 中的實線部分.

(2)請在下圖中用粗實線描出函數y=min{(x-2)2, (x+2)2}的圖像,并寫出該圖像的三條不同性質:

① ;
② ;
③ ;
(3)函數y=min{(x-4)2, (x+2)2}的圖像關于 對稱.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張華隨爸爸來西安游玩,他們還有四個旅游景點沒去,分別是西安以東的兵馬俑和華山,西安以西的乾陵和法門寺。由于僅剩兩天的時間,張華不能游玩所有風景區,于是爸爸讓張華從四張旅游景點圖片(大小、形狀及背面圖案完全相同)中抽簽確定.爸爸將這四張圖片背面朝上洗勻后,讓張華先隨機抽取一張(不放回),再抽取一張,若抽到的兩個景點都在西安以東或都在西安以西,則爸爸帶他到這兩個景點旅游,否則只能去一個景點旅游(兵馬俑、華山、乾陵、法門寺這四張圖片分別用B,H,Q,F表示).
(1)求張華抽到景點兵馬俑的圖片的概率;
(2)請你用列表或畫樹狀圖的方法求張華能去兩個景點旅游的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
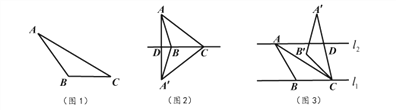
【題目】我們定義:如果一個三角形一條邊上的高等于這條邊,那么這個三角形叫做“等高底”三角形,這條邊叫做這個三角形的“等底”。
(1)概念理解:
如圖1,在![]() 中,
中,![]() ,
,![]() .
.![]() ,試判斷
,試判斷![]() 是否是“等高底”三角形,請說明理由.
是否是“等高底”三角形,請說明理由.
(2)問題探究:
如圖2, ![]() 是“等高底”三角形,
是“等高底”三角形,![]() 是“等底”,作
是“等底”,作![]() 關于
關于![]() 所在直線的對稱圖形得到
所在直線的對稱圖形得到![]() ,連結
,連結![]() 交直線
交直線![]() 于點
于點![]() .若點
.若點![]() 是
是![]() 的重心,求
的重心,求![]() 的值.
的值.
(3)應用拓展:
如圖3,已知![]() ,
,![]() 與
與![]() 之間的距離為2.“等高底”
之間的距離為2.“等高底”![]() 的“等底”
的“等底” ![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 上
上![]() 的
的![]() 倍.將
倍.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得到
得到![]() ,
,![]() 所在直線交
所在直線交![]() 于點
于點![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com