
已知a、b、c、d滿足a<-1<b<0<c<1<d,且|a+1|=|b+1|,|1-c|=|1-d|,求a+b+c+d的值.
|
解:此題應根據a、b、c、d的取值范圍來去掉絕對值符號,從而找出a與b,c與d的關系,然后求解 因為a<-1 所以a+1<-1+1=0 即a+1<0 所以|a+1|=-(a+1)=-a-1 又因為-1<b,所以-1+1<b+1 即b+1>0,所以|b+1|=b+1 因為|a+1|=|b+1| 即-a-1=b+1 所以-a-1+(a-1)=b+1+(a-1) 即a+b=-2 同理|1-c|=1-c,|1-d|=d-1 又因為|1-c|=|1-d| 即1-c=d-1 所以1-c-(1-c)=d-1-(1-c) 即0=c+d-2,0+2=c+d-2+2 所以c+d=2 所以a+b+c+d=-2+2=0 說明:此題不能求出a、b、c、d的值,而是一種整體的處理方法,先求出a+b的值,再求出c+d的值,這樣a+b+c+d的值就可以求出來,要注意這種整體求值的方法. |


科目:初中數學 來源: 題型:
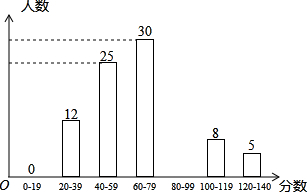
 12、陽光中學舉行應用數學知識競賽.已知競賽成績都是整數,試題滿分為140分,現從參賽學生中隨機抽取100名學生的成績進行統計分析,得到如下圖:
12、陽光中學舉行應用數學知識競賽.已知競賽成績都是整數,試題滿分為140分,現從參賽學生中隨機抽取100名學生的成績進行統計分析,得到如下圖:查看答案和解析>>
科目:初中數學 來源: 題型:
| x | -6 | -5 | -4 | -3 | -2 | -1 | 2 | 3 | 4 | 5 | 6 | … |
| y | 1 | 1.2 | 1.5 | 2 | 3 | 6 | -3 | -2 | -1.5 | -1.2 | -1 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 分數段 | 0~19 | 20~39 | 40~59 | 60~79 | 80~99 | 100~119 | 120~140 |
| 人數 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com