
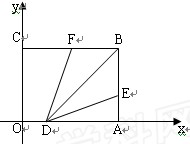
如圖,以矩形 的頂點
的頂點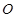 為原點,
為原點, 所在的直線為
所在的直線為 軸,
軸,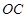 所在的直線為
所在的直線為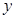 軸,
軸,
建立平面直角坐標系.已知
 為
為 上一動點,點
上一動點,點 以1cm/s的速
以1cm/s的速
度從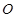 點出發向
點出發向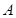 點運動,
點運動,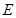 為
為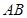 上一動點,點
上一動點,點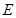 以1cm/s的速度從
以1cm/s的速度從 點出發向點
點出發向點 運
運
動.
(1)試寫出多邊形 的面積
的面積 (
(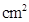 )與運動時間
)與運動時間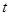 (
(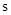 )之間的函數關系式;
)之間的函數關系式;
(2)在(1)的條件下,當多邊形 的面積最小時,在坐標軸上是否存在點
的面積最小時,在坐標軸上是否存在點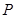 ,使得
,使得 為等腰三角形?若存在,求出點
為等腰三角形?若存在,求出點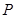 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)在某一時刻將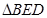 沿著
沿著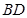 翻折,使得點
翻折,使得點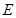 恰好落在
恰好落在 邊的點
邊的點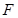 處.求出此時時間t的值.若此時在
處.求出此時時間t的值.若此時在 軸上存在一點
軸上存在一點 在
在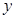 軸上存在一點
軸上存在一點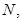
使得四邊形 的周長最小,試求出此時點
的周長最小,試求出此時點 點
點 的坐標.
的坐標.
.(1)∵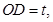 ∴
∴
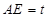

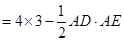
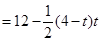
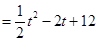 ………………………………………………………3分
………………………………………………………3分
(2)∵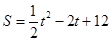
∴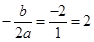
∴當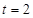 時,
時,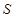 有最小值
有最小值
此時: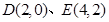
①當 在
在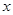 軸上時,設
軸上時,設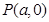
此時: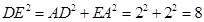
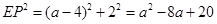
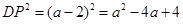
∴當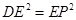 時,
時,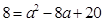
∴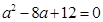
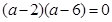
∴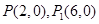
∵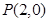 與
與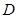 重合 ∴舍去
重合 ∴舍去
當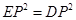 時,
時,
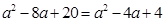
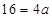
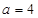
∴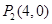
當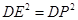 時,
時,
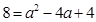
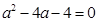
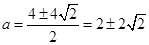
∴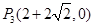
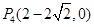
②當 在
在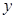 軸上時,設
軸上時,設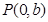
則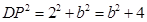
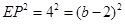
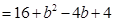
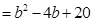
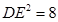
∴當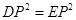 時,
時,

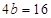
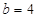
∴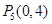
當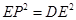 時,
時,
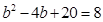
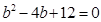
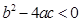 ,∴無解.
,∴無解.
當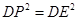 時,
時,
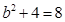
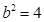
∴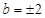
∴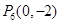 (舍
(舍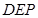 三點重合)
三點重合)
∴綜上共有6個這樣的 點
點
使得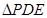 為等腰三角形.
為等腰三角形.
即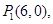
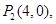

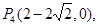

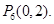
③設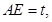 則
則
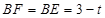
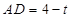
∴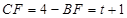
過 作
作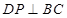 于
于
則: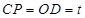
∴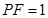
又
∴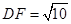
∴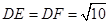
∴在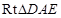 中,
中,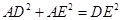
∴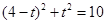
∴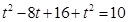
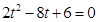
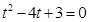
∴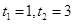 (舍)
(舍)
∴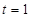 ··································9分
··································9分
∴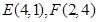
如圖,∵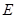 關于
關于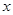 軸的對稱點
軸的對稱點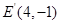 ,
,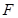 關于
關于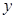 軸的對稱點
軸的對稱點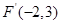
則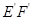 與
與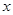 軸,
軸,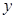 軸的焦點即為
軸的焦點即為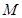 點,
點,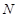 點。
點。
延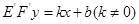
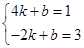 ∴
∴
∴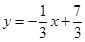 ··········································10分
··········································10分
∴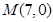 ,
,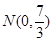 ·············································12分
·············································12分
【解析】略


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
如圖1,矩形![]() 的頂點
的頂點![]() 為原點,點
為原點,點![]() 在
在![]() 上,把
上,把![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,點
處,點![]() 坐標分別為
坐標分別為![]() 和
和![]() ,拋物線
,拋物線![]() 過點
過點![]() .
.

1.求![]() 兩點的坐標及該拋物線的解析式;
兩點的坐標及該拋物線的解析式;
2.如圖2,長、寬一定的矩形![]() 的寬
的寬![]() ,點
,點![]() 沿(1)中的拋物線滑動,在滑動過程中
沿(1)中的拋物線滑動,在滑動過程中![]() 軸,且
軸,且![]() 在
在![]() 的下方,當
的下方,當![]() 點橫坐標為-1時,點
點橫坐標為-1時,點![]() 距離
距離![]() 軸
軸![]() 個單位,當矩形
個單位,當矩形![]() 在滑動過程中被
在滑動過程中被![]() 軸分成上下兩部分的面積比為2:3時,求點
軸分成上下兩部分的面積比為2:3時,求點![]() 的坐標;
的坐標;
3.如圖3,動點![]() 同時從點
同時從點![]() 出發,點
出發,點![]() 以每秒3個單位長度的速度沿折線
以每秒3個單位長度的速度沿折線![]() 按
按![]() 的路線運動,點
的路線運動,點![]() 以每秒8個單位長度的速度沿折線
以每秒8個單位長度的速度沿折線![]() 按
按![]() 的路線運動,當
的路線運動,當![]() 兩點相遇時,它們都停止運動.設
兩點相遇時,它們都停止運動.設![]() 同時從點
同時從點![]() 出發
出發![]() 秒時,
秒時,![]() 的面積為
的面積為![]() .①求出
.①求出![]() 與
與![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍:②設
的取值范圍:②設![]() 是①中函數
是①中函數![]() 的最大值,那么
的最大值,那么![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,以矩形的頂點
為原點,
所在的直線為
軸,
所在的直線為
軸,
建立平面直角坐標系.已知為
上一動點,點
以1cm/s的速
度從點出發向
點運動,
為
上一動點,點
以1cm/s的速度從
點出發向點
運
動.
(1)試寫出多邊形的面積
(
)與運動時間
(
)之間的函數關系式;
(2)在(1)的條件下,當多邊形的面積最小時,在坐標軸上是否存在點
,使得
為等腰三角形?若存在,求出點
的坐標;若不存在,請說明理由;
(3)在某一時刻將沿著
翻折,使得點
恰好落在
邊的點
處.求出此時時間t的值.若此時在
軸上存在一點
在
軸上存在一點
使得四邊形的周長最小,試求出此時點
點
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
 的頂點
的頂點 為原點,
為原點, 所在的直線為
所在的直線為 軸,
軸, 所在的直線為
所在的直線為 軸,
軸,
 為
為 上一動點,點
上一動點,點 以1cm/s的速
以1cm/s的速 點出發向
點出發向 點運動,
點運動, 為
為 上一動點,點
上一動點,點 以1cm/s的速度從
以1cm/s的速度從 點出發向點
點出發向點 運
運
 的面積
的面積 (
( )與運動時間
)與運動時間 (
( )之間的函數關系式;
)之間的函數關系式; 的面積最小時,在坐標軸上是否存在點
的面積最小時,在坐標軸上是否存在點 ,使得
,使得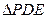 為等腰三角形?若存在,求出點
為等腰三角形?若存在,求出點 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由; 沿著
沿著 翻折,使得點
翻折,使得點 恰好落在
恰好落在 邊的點
邊的點 處.求出此時時間t的值.若此時在
處.求出此時時間t的值.若此時在 軸上存在一點
軸上存在一點 在
在 軸上存在一點
軸上存在一點
 的周長最小,試求出此時點
的周長最小,試求出此時點 點
點 的坐標.
的坐標.查看答案和解析>>
科目:初中數學 來源:2011屆安徽省安慶市中考模擬一模數學卷 題型:解答題
如圖,以矩形 的頂點
的頂點 為原點,
為原點, 所在的直線為
所在的直線為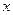 軸,
軸, 所在的直線為
所在的直線為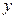 軸,
軸,
建立平面直角坐標系.已知
 為
為 上一動點,點
上一動點,點 以1cm/s的速
以1cm/s的速
度從 點出發向
點出發向 點運動,
點運動, 為
為
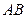 上一動點,點
上一動點,點 以1cm/s的速度從
以1cm/s的速度從 點出發向點
點出發向點 運
運
動.
(1)試寫出多邊形 的面積
的面積 (
( )與運動時間
)與運動時間 (
( )之間的函數關系式;
)之間的函數關系式;
(2)在(1)的條件下,當多邊形 的面積最小時,在坐標軸上是否存在點
的面積最小時,在坐標軸上是否存在點 ,使得
,使得 為等腰三角形?若存在,求出點
為等腰三角形?若存在,求出點 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)在某一時刻將 沿著
沿著 翻折,使得點
翻折,使得點 恰好落在
恰好落在 邊的點
邊的點 處.求出此時時間t的值.若此時在
處.求出此時時間t的值.若此時在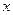 軸上存在一點
軸上存在一點 在
在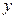 軸上存在一點
軸上存在一點
使得四邊形 的周長最小,試求出此時點
的周長最小,試求出此時點 點
點 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com