
【題目】某電視臺(tái)為了解本地區(qū)電視節(jié)目的收視情況,對(duì)部分市民開展了“你最喜愛的電視節(jié)目”的問卷調(diào)查(每人只填寫一項(xiàng)),根據(jù)收集的數(shù)據(jù)繪制了兩幅不完整的統(tǒng)計(jì)圖(如圖所示),根據(jù)要求回答下列問題:
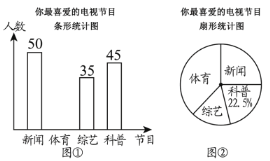
(1)本次問卷調(diào)查共調(diào)查了________名觀眾;圖②中最喜愛“體育節(jié)目”的扇形圓心角度數(shù)是________.
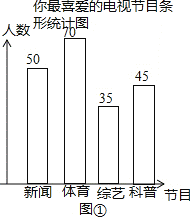
(2)補(bǔ)全圖①中的條形統(tǒng)計(jì)圖;
(3)現(xiàn)有最喜愛“新聞節(jié)目”(記為![]() ),“體育節(jié)目”(記為
),“體育節(jié)目”(記為![]() ),“綜藝節(jié)目”(記為
),“綜藝節(jié)目”(記為![]() ),“科普節(jié)目”(記為
),“科普節(jié)目”(記為![]() )的觀眾各一名,電視臺(tái)要從四人中隨機(jī)抽取兩人參加聯(lián)誼活動(dòng),請(qǐng)用列表或畫樹狀圖的方法,求出恰好抽到最喜愛“
)的觀眾各一名,電視臺(tái)要從四人中隨機(jī)抽取兩人參加聯(lián)誼活動(dòng),請(qǐng)用列表或畫樹狀圖的方法,求出恰好抽到最喜愛“![]() ”和“
”和“![]() ”兩位觀眾的概率.
”兩位觀眾的概率.
【答案】(1)200;126°;(2)見解析;(3)![]()
【解析】
(1)用最喜愛“科普節(jié)目”的人數(shù)除以它所占的百分比即可得到調(diào)查的總?cè)藬?shù),再算出最喜愛“體育節(jié)目”的人數(shù)及所占的百分比,然后用360度乘最喜愛“體育節(jié)目”的人數(shù)所占的百分比即可得到“體育節(jié)目”在扇形統(tǒng)計(jì)圖中所對(duì)應(yīng)的圓心角的度數(shù);
(2)由(1)求得的最喜愛“體育節(jié)目”的人數(shù)即可補(bǔ)全條形統(tǒng)計(jì)圖;
(3)畫樹狀圖展示所有12種等可能的結(jié)果數(shù),再找出抽到最喜愛“B”和“C”兩位觀眾的結(jié)果數(shù),然后根據(jù)概率公式求解.
解:(1)本次問卷調(diào)查的總?cè)藬?shù)為:45÷22.5%=200(人),
∴最喜愛“體育節(jié)目”類節(jié)目的人數(shù)為200(50+35+45)=70(人),
則圖②中最喜愛“體育節(jié)目”的人數(shù)占調(diào)查總?cè)藬?shù)的百分比為70÷200×100%=35%,
∴“體育節(jié)目”在扇形統(tǒng)計(jì)圖中所對(duì)應(yīng)的圓心角的度數(shù)為![]() ,
,
故答案為:200;![]() ;
;
(2)由(1)得:最喜愛“體育節(jié)目”類節(jié)目的人數(shù)為70人,
補(bǔ)全圖①中的條形統(tǒng)計(jì)圖如圖①所示:
(3)根據(jù)題意可畫樹狀圖為:

共有12種等可能的結(jié)果數(shù),恰好抽到最喜愛“B”和“C”兩位觀眾的結(jié)果數(shù)為2,
所以P(恰好抽到最喜愛“B”和“C”兩位觀眾)=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2018年5月3日,中國(guó)科學(xué)院在上海發(fā)布了中國(guó)首款人工智能芯片:寒武紀(jì)(MLU100),該芯片在平衡模式下的等效理論峰值速度達(dá)每秒128 000 000 000 000次定點(diǎn)運(yùn)算,將數(shù)
128 000 000 000 000用科學(xué)計(jì)數(shù)法表示為( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點(diǎn)A按順時(shí)針方向旋轉(zhuǎn)得到的.連接BE、CF相交于點(diǎn)D.
(1)求證:BE=CF.
(2)當(dāng)四邊形ACDE為菱形時(shí),求BD的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明在一次數(shù)學(xué)興趣小組活動(dòng)中,對(duì)一個(gè)數(shù)學(xué)問題作如下探究:
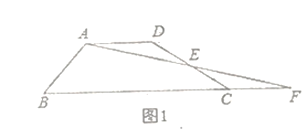
問題情境:(1)如圖1,四邊形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊的中點(diǎn),連接
邊的中點(diǎn),連接![]() 并延長(zhǎng)交
并延長(zhǎng)交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,求證:
,求證:![]() ;(
;(![]() 表示面積)
表示面積)
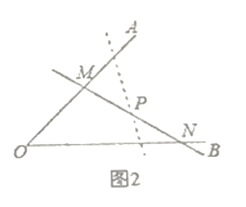
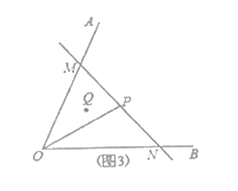
問題遷移:(2)如圖2:在已知銳角![]() 內(nèi)有一個(gè)定點(diǎn)
內(nèi)有一個(gè)定點(diǎn)![]() .過點(diǎn)
.過點(diǎn)![]() 任意作一條直線
任意作一條直線![]() 分別交射線
分別交射線![]() 于點(diǎn)
于點(diǎn)![]() .小明將直線
.小明將直線![]() 繞著點(diǎn)
繞著點(diǎn)![]() 旋轉(zhuǎn)的過程中發(fā)現(xiàn),
旋轉(zhuǎn)的過程中發(fā)現(xiàn),![]() 的面積存在最小值,請(qǐng)問當(dāng)直線
的面積存在最小值,請(qǐng)問當(dāng)直線![]() 在什么位置時(shí),
在什么位置時(shí),![]() 的面積最小,并說明理由.
的面積最小,并說明理由.
實(shí)際應(yīng)用:(3)如圖3,若在道路![]() 之間有一村莊
之間有一村莊![]() 發(fā)生疫情,防疫部門計(jì)劃以公路
發(fā)生疫情,防疫部門計(jì)劃以公路![]() 和經(jīng)過防疫站
和經(jīng)過防疫站![]() 的一條直線
的一條直線![]() 為隔離線,建立個(gè)面積最小的三角形隔離區(qū)
為隔離線,建立個(gè)面積最小的三角形隔離區(qū)![]() ,若測(cè)得
,若測(cè)得![]() 試求
試求![]() 的面積.(結(jié)果保留根號(hào))(參考數(shù)據(jù):
的面積.(結(jié)果保留根號(hào))(參考數(shù)據(jù):![]() )
)
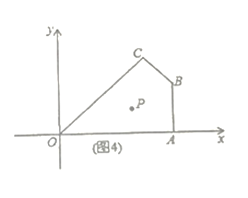
拓展延伸:(4)如圖4,在平面直角坐標(biāo)系中,![]() 為坐標(biāo)原點(diǎn),點(diǎn)
為坐標(biāo)原點(diǎn),點(diǎn)![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 與四邊形
與四邊形![]() 一組對(duì)邊相交,將四邊形
一組對(duì)邊相交,將四邊形![]() 分成兩個(gè)四邊形,求其中以點(diǎn)
分成兩個(gè)四邊形,求其中以點(diǎn)![]() 為頂點(diǎn)的四邊形面積的最大值.
為頂點(diǎn)的四邊形面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,拋物線y=mx2﹣6mx+9m+1(m≠0).
(1)求拋物線的頂點(diǎn)坐標(biāo);
(2)若拋物線與x軸的兩個(gè)交點(diǎn)分別為A和B點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),且AB=4,求m的值.
(3)已知四個(gè)點(diǎn)C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若拋物線與線段CD和線段EF都沒有公共點(diǎn),請(qǐng)直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】規(guī)定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
據(jù)此判斷下列等式成立的是 (寫出所有正確的序號(hào))
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
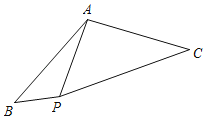
【題目】如圖,線段AB繞著點(diǎn)A逆時(shí)針方向旋轉(zhuǎn)120°得到線段AC,點(diǎn)B對(duì)應(yīng)點(diǎn)C,在∠BAC的內(nèi)部有一點(diǎn)P,PA=8,PB=4,PC=4![]() ,則線段AB的長(zhǎng)為_____.
,則線段AB的長(zhǎng)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一副三角尺按如圖①方式拼接:含30°角的三角尺的長(zhǎng)直角邊與含45°角的三角尺的斜邊恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2![]() ,P是AC上的一個(gè)動(dòng)點(diǎn).
,P是AC上的一個(gè)動(dòng)點(diǎn).

(1)當(dāng)PD=BC時(shí),求∠PDA的度數(shù);
(2)如圖②,若E是CD的中點(diǎn),求△DEP周長(zhǎng)的最小值;
(3)如圖③,當(dāng)DP平分∠ADC時(shí),在△ABC內(nèi)存在一點(diǎn)Q,使得∠DQC=∠DPC,且CQ=![]() ,求PQ的長(zhǎng).
,求PQ的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
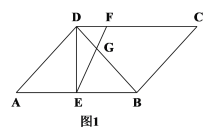
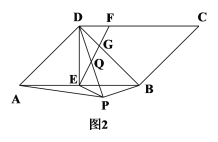
【題目】在平行四邊形ABCD中,AD=BD,E為AB的中點(diǎn),F為CD上一點(diǎn),連接EF交BD于G.
(1)如圖1,若DF=DG=2,AB=8,求EF的長(zhǎng);
(2)如圖2,∠ADB=90°,點(diǎn)P為平行四邊形ABCD外部一點(diǎn),且AP=AD,連接BP、DP、EP,DP交EF于點(diǎn)Q,若BP⊥DP,EF⊥EP,求證:DQ=PQ.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com