
【題目】如圖1,在平面直角坐標(biāo)系中,拋物線![]() 與x軸交于點(diǎn)A、B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,過點(diǎn)C作CD∥x軸,且交拋物線于點(diǎn)D,連接AD,交y軸于點(diǎn)E,連接AC.
與x軸交于點(diǎn)A、B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,過點(diǎn)C作CD∥x軸,且交拋物線于點(diǎn)D,連接AD,交y軸于點(diǎn)E,連接AC.

(1)求S△ABD的值;
(2)如圖2,若點(diǎn)P是直線AD下方拋物線上一動(dòng)點(diǎn),過點(diǎn)P作PF∥y軸交直線AD于點(diǎn)F,作PG∥AC交直線AD于點(diǎn)G,當(dāng)△PGF的周長最大時(shí),在線段DE上取一點(diǎn)Q,當(dāng)PQ+![]() QE的值最小時(shí),求此時(shí)PQ+
QE的值最小時(shí),求此時(shí)PQ+ ![]() QE的值;
QE的值;
(3)如圖3,M是BC的中點(diǎn),以CM為斜邊作直角△CMN,使CN∥x軸,MN∥y軸,將△CMN沿射線CB平移,記平移后的三角形為△C′M′N′,當(dāng)點(diǎn)N′落在x軸上即停止運(yùn)動(dòng),將此時(shí)的△C′M′N′繞點(diǎn)C′逆時(shí)針旋轉(zhuǎn)(旋轉(zhuǎn)度數(shù)不超過180°),旋轉(zhuǎn)過程中直線M′N′與直線CA交于點(diǎn)S,與y軸交于點(diǎn)T,與x軸交于點(diǎn)W,請問△CST是否能為等腰三角形?若能,請求出所有符合條件的WN′的長度;若不能,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】試題分析:(1)求出A、B、C的坐標(biāo),由CD∥AB,推出S△DAB=S△ABC=![]() ABOC,由此即可解決問題;
ABOC,由此即可解決問題;
(2)首先說明PF的值最大時(shí),△PFG的周長最大,由PF=![]() ,可知當(dāng)m=
,可知當(dāng)m=![]() =
=![]() 時(shí),PF的值最大,此時(shí)P(
時(shí),PF的值最大,此時(shí)P(![]() ,
, ![]() ),作P關(guān)于直線DE的對(duì)稱點(diǎn)P′,連接P′Q,PQ,作EN∥x軸,QM⊥EN于M,由△QEM∽△EAO,可得
),作P關(guān)于直線DE的對(duì)稱點(diǎn)P′,連接P′Q,PQ,作EN∥x軸,QM⊥EN于M,由△QEM∽△EAO,可得![]() =
=![]() ,推出QM=
,推出QM=![]() QE,推出PQ+
QE,推出PQ+![]() EQ=PQ+QM=P′Q+QM,推出當(dāng)P′、Q、M共線時(shí),PQ+
EQ=PQ+QM=P′Q+QM,推出當(dāng)P′、Q、M共線時(shí),PQ+![]() EQ的值最小,想辦法求出P′的坐標(biāo)即可解決問題;
EQ的值最小,想辦法求出P′的坐標(biāo)即可解決問題;
(3)分四種情形情形討論.
試題解析:解:(1)令y=0,則![]() ,解得x=
,解得x=![]() 或
或![]() ,∴A(
,∴A(![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0, ![]() ),∵CD∥AB,∴S△DAB=S△ABC=
),∵CD∥AB,∴S△DAB=S△ABC=![]() ABOC=
ABOC=![]() ×
×![]() ×
×![]() =
=![]() .
.
(2)如圖2中,設(shè)P(m, ![]() ).
).

∵A(![]() ,0),D(
,0),D(![]() ,
, ![]() ),∴直線AD的解析式為
),∴直線AD的解析式為![]() ,∵PF∥y軸,∴F(m,
,∵PF∥y軸,∴F(m, ![]() ),∵PG⊥DE,∴△PGF的形狀是相似的,∴PF的值最大時(shí),△PFG的周長最大,∵PF=
),∵PG⊥DE,∴△PGF的形狀是相似的,∴PF的值最大時(shí),△PFG的周長最大,∵PF=![]() ﹣(
﹣(![]() )=
)=![]() ,∴當(dāng)m=
,∴當(dāng)m=![]() =
=![]() 時(shí),PF的值最大,此時(shí)P(
時(shí),PF的值最大,此時(shí)P(![]() ,
, ![]() ),作P關(guān)于直線DE的對(duì)稱點(diǎn)P′,連接P′Q,PQ,作EN∥x軸,QM⊥EN于M,∵△QEM∽△EAO,∴
),作P關(guān)于直線DE的對(duì)稱點(diǎn)P′,連接P′Q,PQ,作EN∥x軸,QM⊥EN于M,∵△QEM∽△EAO,∴![]() =
=![]() ,∴QM=
,∴QM=![]() QE,∴PQ+
QE,∴PQ+![]() EQ=PQ+QM=P′Q+QM,∴當(dāng)P′、Q、M共線時(shí),PQ+
EQ=PQ+QM=P′Q+QM,∴當(dāng)P′、Q、M共線時(shí),PQ+![]() EQ的值最小,易知直線PP′的解析式為
EQ的值最小,易知直線PP′的解析式為![]() ,由
,由 ,可得G(
,可得G(![]() ,
, ![]() ),∵PG=GP′,∴P′(
),∵PG=GP′,∴P′(![]() ,
, ![]() ),∴P′M=
),∴P′M=![]() =
=![]() ,∴PQ+
,∴PQ+![]() EQ的最小值為
EQ的最小值為![]() .
.
(3)①如圖3中,當(dāng)CS=CT時(shí),作CK平分∠OCA,作KG⊥AC于G.

易知KO=KG,∵ ![]() =
=![]() =
= =
=![]() =
=![]() ,∴OK=
,∴OK=![]() =
=![]() ,易證∠BWN′=∠OCK,∴tan∠BWN′=tan∠OCK=
,易證∠BWN′=∠OCK,∴tan∠BWN′=tan∠OCK=![]() =
=![]() ,∵BN′=
,∵BN′=![]() ,∴WN′=
,∴WN′=![]() .
.
②如圖4中,當(dāng)TC=TS時(shí),易證∠BWN′=∠OAC,∴tan∠BWN′=tan∠OAC=![]() =
=![]() ,∴WN′=
,∴WN′=![]() ;
;

③如圖5中,當(dāng)TS=TC時(shí),延長N′B交直線AC于Q,作BG⊥AQ于G,QR⊥AB于R.

∵TS=TC,∴∠TSC=∠TCS=∠ACO,∵∠TSC+∠SQN′=90°,∠ACO+∠OAC=90°,∴∠BQA=∠OAC=∠BAQ,∴BA=BQ,∴AG=GQ,設(shè)AQ=a,則易知BG=a,BQ=AB=![]() a,∵
a,∵![]() AQBG=
AQBG=![]() ABQR,∴QR=
ABQR,∴QR=![]() a,BR=
a,BR=![]() a,∴tan∠WBN′=tan∠QBR=
a,∴tan∠WBN′=tan∠QBR=![]() =
=![]() ,∴WN′=
,∴WN′=![]() .
.
④如圖6中,當(dāng)CS=CT時(shí),由①可知,在Rt△BN′W中,tan∠N′BW=![]() =
=![]() ,∴
,∴![]() .
.

綜上所述,滿足條件的WN′的長為![]() 或
或![]() 或
或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,A城氣象臺(tái)測得臺(tái)風(fēng)中心在A城正西方向600km的B處,以每小時(shí)200km的速度向北偏東60°的BC方向移動(dòng),距臺(tái)風(fēng)中心500km的范圍是受臺(tái)風(fēng)影響的區(qū)域
(1)A城是否受這次臺(tái)風(fēng)的影響?
(2)若A城受到這次臺(tái)風(fēng)的影響,那么A城遭受臺(tái)風(fēng)影響有多長時(shí)間?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,方格紙中每個(gè)小方格都是邊長為1的正方形,已知學(xué)校的坐標(biāo)為A(2,2).
(1)請?jiān)趫D中建立適當(dāng)?shù)闹苯亲鴺?biāo)系,并寫出圖書館的坐標(biāo);
(2)若體育館的坐標(biāo)為C(-2,3),請?jiān)谧鴺?biāo)系中標(biāo)出體育館的位置,并順次連接學(xué)校、圖書館、體育館,得到△ABC,求△ABC的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知直線AB和CD相交于點(diǎn)O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度數(shù).
(2)寫出∠DON的余角.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
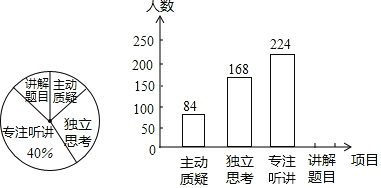
【題目】某市數(shù)學(xué)調(diào)研小組對(duì)老師在講評(píng)試卷中學(xué)生參與的深度與廣度進(jìn)行評(píng)價(jià)調(diào)查,其評(píng)價(jià)項(xiàng)目為“主動(dòng)質(zhì)疑”、“獨(dú)立思考”、“專注聽講”、“講解題目”四項(xiàng),該調(diào)研小組隨機(jī)抽取了若干名初中七年級(jí)學(xué)生的參與情況,繪制成如圖所示的頻數(shù)分布直方圖和扇形統(tǒng)計(jì)圖(均不完整),請根據(jù)圖中所給信息答下列問題:
(1)在這次評(píng)價(jià)中,一共抽查了 名學(xué)生;
(2)請將頻數(shù)分布直方圖補(bǔ)充完整;
(3)如果全市有4000名七年級(jí)學(xué)生,那么在試卷評(píng)講課中,“獨(dú)立思考”的七年級(jí)學(xué)生約有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場購進(jìn)一批LED燈泡與普通白熾燈炮,其進(jìn)價(jià)與標(biāo)價(jià)如下表,該商場購進(jìn)LED燈泡與普通白熾燈炮共300個(gè),LED燈泡按標(biāo)價(jià)進(jìn)行銷售,而普通白熾燈炮按標(biāo)價(jià)打九折銷售,銷售完這批燈泡后可以獲利3200元。
(1)求該商場購進(jìn)LED燈泡與普通白熾燈泡的數(shù)量分別為多少個(gè)?
(2)由于春節(jié)期間熱銷,很快將兩種燈泡銷售完,若該商場計(jì)劃再次購進(jìn)兩種燈泡120個(gè),并在不打折的情況下銷售完,若銷售完這批燈泡的獲利不超過總進(jìn)貨價(jià)的28%,則最多購進(jìn)LED燈泡多少個(gè)?
LED燈泡 | 普通白熾燈泡 | |
進(jìn)價(jià)(元) | 45 | 25 |
標(biāo)價(jià)(元) | 60 | 30 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,平行四邊形ABCD中,E,F是對(duì)角線BD上的兩點(diǎn),如果添加一個(gè)條件使△ABE≌△CDF,則添加的條件不能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知有一塊等腰三角形紙板,在它的兩腰上各有一點(diǎn)E和F,把這兩點(diǎn)分別與底邊中點(diǎn)連結(jié),并沿著這兩條線段剪下兩個(gè)三角形,所得的這兩個(gè)三角形相似,剩余部分(四邊形)的四條邊的長度如圖所示,那么原等腰三角形的底邊長為( )

A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知反比例函數(shù)![]() 的圖象經(jīng)過點(diǎn)A(1,3).
的圖象經(jīng)過點(diǎn)A(1,3).
(1)試確定此反比例函數(shù)的解析式;
(2)當(dāng)![]() =2時(shí), 求y的值;
=2時(shí), 求y的值;
(3)當(dāng)自變量![]() 從5增大到8時(shí),函數(shù)值y是怎樣變化的?
從5增大到8時(shí),函數(shù)值y是怎樣變化的?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com