Question

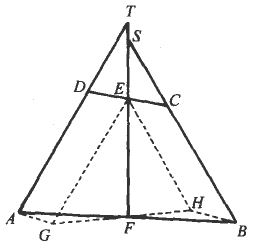
如圖，在四邊形ABCD中，AD＝BC，E、F分別是CD、AB的中點，直線EF分別交BC、AD的延長線于點S、T．求證：∠ATS＝∠BSF．

Answer 1

答案：
解析：

證明：過點E作EGAD，EHBC，連結GH、AG、BH，則四邊形DEGA、EHBC均為平行四邊形． 　　∴AGDE，BHEC， 　　又∵DE＝EC， 　　∴AGBH． 　　∴四邊形AGBH是平行四邊形． 　　又∵F是AB中點， 　　∴H、F、G三點共線且F是GH中點． 　　∴EF是△EGH的中線． 　　又∵EG＝AD＝BC＝EH， 　　∴EF平分∠GEH． 　　又∵∠GEF＝∠ATS，∠HEF＝∠BSF， 　　∴∠ATS＝∠BSF．

提示：

點悟：由于∠ATS和∠BSF不在同一個三角形內，又不可能在兩個全等的三角形內，又沒有直接的聯系，故需通過添加輔助線使兩個角有一定的關系，由于所給的條件和中點均在四邊形ABCD內，因此可設想把∠ATS和∠BSF都移到四邊形ABCD內． 　　點撥：在幾何命題論證中，要注意通過添加適當的輔助線，將分散的、遠離的元素，通過變化和轉換，使它們相對集中，從而導出要求的結論．