【題目】下面是小明設計的“在一個平行四邊形內作菱形”的尺規作圖過程．
已知：四邊形
是平行四邊形．
求作：菱形
（點
在
上，點
在
上）．
作法：①以
為圓心，
長為半徑作弧，交于點；
②以
為圓心，長為半徑作弧，交于點；
③連接
．所以四邊形為所求作的菱形．
根據小明設計的尺規作圖過程，
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：∵
，
，
∴ ＝ ．
在
中，
．
即
．
∴四邊形為平行四邊形．
∵，
∴四邊形為菱形（ ）（填推理的依據）．
初中暑期銜接系列答案科目：初中數學 來源： 題型：
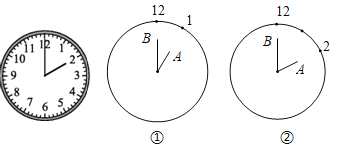
【題目】如圖，有一時鐘，時針OA長為6cm，分針OB長為8cm，△OAB隨著時間的變化不停地改變形狀．求：
（1）如圖①，13點時，△OAB的面積是多少？
（2）如圖②，14點時，△OAB的面積比13點時增大了還是減少了？為什么？
（3）問多少整點時，△OAB的面積最大？最大面積是多少？請說明理由．
（4）設∠BOA＝α（0°≤α≤180°），試歸納α變化時△OAB的面積有何變化規律（不證明）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，點D是BC的中點，點E、F分別在線段AD及其延長線上，且DE=DF，給出下列條件：①BE⊥EC；②AB=AC；③BF∥EC；從中選擇一個條件使四邊形BECF是菱形，你認為這個條件是_______(只填寫序號)．
查看答案和解析>>
科目：初中數學 來源： 題型：
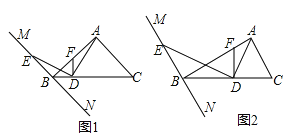
【題目】在Rt△ABC中，∠BAC=90°，過點B的直線MN∥AC，D為BC邊上一點，連接AD，作DE⊥AD交MN于點E，連接AE．
（1）如圖①，當∠ABC=45°時，求證：AD=DE；理由；
（2）如圖②，當∠ABC=30°時，線段AD與DE有何數量關系？并請說明理由；
（3）當∠ABC=α時，請直接寫出線段AD與DE的數量關系．（用含α的三角函數表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
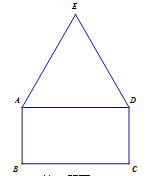
【題目】如圖所示，矩形ABCD的邊長AB＝2，BC＝2
，△ADE為正三角形．
若半徑為R的圓能夠覆蓋五邊形ABCDE（即五邊形ABCDE的每個頂點都在圓內或圓上），則R的最小值是（ ）
A.2B.4C.2.8D.2.5
查看答案和解析>>
科目：初中數學 來源： 題型：
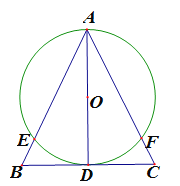
【題目】如圖，△ABC中，AB=AC，AD⊥BC于D，以AD為直徑的⊙O交AB于E，交AC于F．
（1）求證：BE=CF；
（2）若AE=4，BC=
，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在菱形
中，對角線
與
相交于點
，
，
，在菱形的外部以
為邊作等邊三角形
．點
是對角線上一動點（點不與點
重合），將線段
繞點
順時針方向旋轉
得到線段
，連接
．
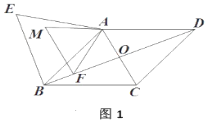
（1）線段
的長為__________；
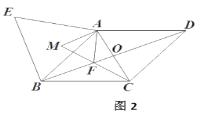
（2）如圖2，當點在線段
上，且點
，，
三點在同一條直線上時，求證：
；
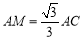（3）連接
．若
的周長為
，請直接寫出
的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=ax2+bx+c交x軸于A（﹣1，0），B（3，0），交y軸的負半軸于C，頂點為D．下列結論：①2a+b=0；②2c＜3b；③當m≠1時，a+b＜am2+bm；④當△ABD是等腰直角三角形時，則a=
；⑤當△ABC是等腰三角形時，a的值有3個．其中正確的有（ ）個．
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
