
如圖,拋物線 交
交 軸于
軸于 兩點(
兩點( 的左側),交
的左側),交 軸于點
軸于點 ,頂點為
,頂點為 。
。

(1)求點 的坐標;
的坐標;
(2)求四邊形 的面積;
的面積;
(3)拋物線上是否存在點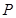 ,使得
,使得 ,若存在,請求出點
,若存在,請求出點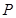 的坐標;若不存在,請說明理由。
的坐標;若不存在,請說明理由。
(1) A(-1,0);B(3,0);C(0,3);(2)9;(3) 存在這樣的點P,P點的坐標為(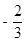 ,
,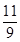 )或(
)或(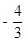 ,
,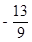 ).
).
【解析】
試題分析:(1)在拋物線的解析式中,令x=0可以求出點C的坐標,令x=0可以求出A、B點的坐標.
(2)過D作DE⊥AB,垂足為E,則四邊形ABDC的面積就是: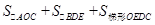
(3)根據條件判定△BCD是直角三角形,再依據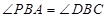 求出
求出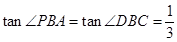 .設P點坐標為(m,-m2+2m+3),分兩種情況討論:(1)當P點在x 軸上方時,(2)當P點在x軸下方時,解直角三角形即可求出m的值,從而確定點P的坐標.
.設P點坐標為(m,-m2+2m+3),分兩種情況討論:(1)當P點在x 軸上方時,(2)當P點在x軸下方時,解直角三角形即可求出m的值,從而確定點P的坐標.
試題解析:(1)當x=0時,y=-x2+2x+3=3;
當y=0時,0=-x2
解得:x1=-1、x2=3;
故A(-1,0);B(3,0);C(0,3).
(2)
∴D點坐標為(1,4)
過點D作DE⊥x軸于E
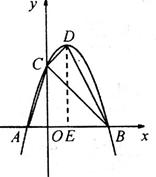
∴OE=1,DE=4
∴BE=OB-OE=2
∵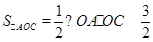 ,
, ,
,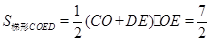
∴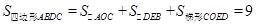
(3)假設存在這樣的點P
過點C作CF⊥DE于F
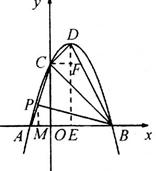
∴CF=1,DF=1
∴∠DCF=45°,CD=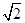
∵OC=3=OB,
∴∠CBO=45°,BC=
∵CF∥x軸
∴∠FCB=∠CBO=45°,
∴∠DCB=90°
在Rt△BCD中,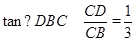
∴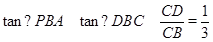
設P點坐標為(m,-m2+2m+3),
過點P作PM⊥AB于M
當P點在x軸上方時,PM=-m2+2m+3,BM=3-m
在Rt△PBM中,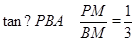 ,即
,即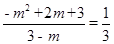
∴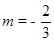 或
或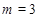 (舍去)
(舍去)
∴P點坐標為(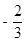 ,
,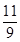 )
)
當P點在x軸下方時,PM=-m2-2m-3,BM=3-m
在Rt△PBM中,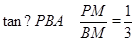 ,即
,即
∴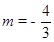 或
或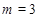 (舍去)
(舍去)
∴P點坐標為(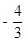 ,
,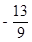 )
)
綜上,存在這樣的點P,P點的坐標為(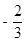 ,
,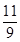 )或(
)或(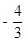 ,
,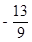 )
)
考點: 二次函數綜合題.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
如圖,已知拋物線 交 軸于A、B兩點,交 軸于點C,拋物線的對稱軸交 軸于點E,點B的坐標為( ,0).
(1)求拋物線的對稱軸及點A的坐標;
(2)在平面直角坐標系 中是否存在點P,與A、B、C三點構成一個平行四邊形?若存在,請寫出點P的坐標;若不存在,請說明理由;
(3)連結CA與拋物線的對稱軸交于點D,在拋物線上是否存在點M,使得直線CM把四邊形DEOC分成面積相等的兩部分?若存在,請求出直線CM的解析式;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,拋物線與 軸交于
軸交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)兩點,且
,0)兩點,且![]() ,與
,與![]() 軸交于點
軸交于點![]() ,其中
,其中![]() 是方程
是方程![]() 的兩個根。(14分)
的兩個根。(14分)
(1)求拋物線的解析式;
 (2)點
(2)點![]() 是線段
是線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
(3)點![]() 在(1)中拋物線上,
在(1)中拋物線上,
點 為拋物線上一動點,在
為拋物線上一動點,在![]() 軸上是
軸上是
否存在點 ,使以
,使以![]() 為頂
為頂
點的四邊形是平行四邊形,如果存在,
求出所有滿足條件的點![]() 的坐標,
的坐標,
若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
 軸交于
軸交于 (
( ,0)、
,0)、 (
( ,0)兩點,且
,0)兩點,且 ,與
,與 軸交于點
軸交于點 ,其中
,其中 是方程
是方程 的兩個根。
的兩個根。 是線段
是線段 上的一個動點,過點
上的一個動點,過點 作
作 ∥
∥ ,交
,交 于點
于點 ,連接
,連接 ,當
,當 的面積最大時,求點
的面積最大時,求點 的坐標;
的坐標; 在(1)中拋物線上,點
在(1)中拋物線上,點 為拋物線上一動點,在
為拋物線上一動點,在 軸上是否存在點
軸上是否存在點 ,使以
,使以 為頂點的四邊形是平行四邊形,如果存在,求出所有滿足條件的點
為頂點的四邊形是平行四邊形,如果存在,求出所有滿足條件的點 的坐標,若不存在,請說明理由。
的坐標,若不存在,請說明理由。查看答案和解析>>
科目:初中數學 來源:2010年高級中等學校招生全國統一考試數學卷(山東萊蕪) 題型:解答題
(本題滿分12分)
如圖,在平面直角坐標系中,已知拋物線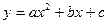 交
交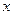 軸于
軸于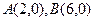 兩點,交
兩點,交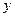 軸于點
軸于點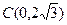 .
.
(1)求此拋物線的解析式; (2)若此拋物線的對稱軸與直線
(2)若此拋物線的對稱軸與直線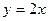 交于點D,作⊙D與x軸相切,⊙D交
交于點D,作⊙D與x軸相切,⊙D交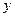 軸于點E、F兩點,求劣弧EF的長;
軸于點E、F兩點,求劣弧EF的長;
(3)P為此拋物線在第二象限圖像上的一點,PG垂直于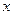 軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
查看答案和解析>>
科目:初中數學 來源:2010年高級中等學校招生全國統一考試數學卷(四川內江) 題型:解答題
(本題滿分12分)
如圖,在平面直角坐標系中,已知拋物線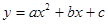 交
交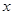 軸于
軸于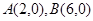 兩點,交
兩點,交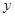 軸于點
軸于點 .
.
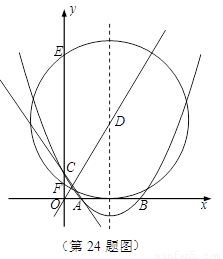
(1)求此拋物線的解析式;
 (2)若此拋物線的對稱軸與直線
(2)若此拋物線的對稱軸與直線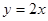 交于點D,作⊙D與x軸相切,⊙D交
交于點D,作⊙D與x軸相切,⊙D交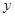 軸于點E、F兩點,求劣弧EF的長;
軸于點E、F兩點,求劣弧EF的長;
(3)P為此拋物線在第二象限圖像上的一點,PG垂直于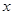 軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com