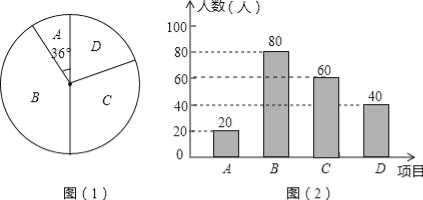
【題目】某學校為了增強學生體質，決定開設以下體育課外活動項目：A．籃球 B．乒乓球C．羽毛球 D．足球，為了解學生最喜歡哪一種活動項目，隨機抽取了部分學生進行調查，并將調查結果繪制成了兩幅不完整的統計圖，請回答下列問題：
（1）這次被調查的學生共有 人；
（2）請你將條形統計圖（2）補充完整；
（3）在平時的乒乓球項目訓練中，甲、乙、丙、丁四人表現優秀，現決定從這四名同學中任選兩名參加乒乓球比賽，求恰好選中甲、乙兩位同學的概率（用樹狀圖或列表法解答）
【答案】（1）200，（2）圖形見解析（3）
【解析】
試題（1）由喜歡籃球的人數除以所占的百分比即可求出總人數；
（2）由總人數減去喜歡A，B及D的人數求出喜歡C的人數，補全統計圖即可；
（3）根據題意列出表格，得出所有等可能的情況數，找出滿足題意的情況數，即可求出所求的概率．
試題解析：（1）根據題意得：20÷
=200（人），
則這次被調查的學生共有200人；
（2）補全圖形，如圖所示：
（3）列表如下：
甲 | 乙 | 丙 | 丁 | |
甲 | ﹣﹣﹣ | （乙，甲） | （丙，甲） | （丁，甲） |
乙 | （甲，乙） | ﹣﹣﹣ | （丙，乙） | （丁，乙） |
丙 | （甲，丙） | （乙，丙） | ﹣﹣﹣ | （丁，丙） |
丁 | （甲，丁） | （乙，丁） | （丙，丁） | ﹣﹣﹣ |
所有等可能的結果為12種，其中符合要求的只有2種，
則P=
．
科目：初中數學 來源： 題型：
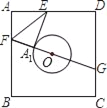
【題目】如圖，已知正方形紙片ABCD的邊是⊙O半徑的4倍，點O是正方形ABCD的中心，將紙片保持圖示方式折疊，使EA1恰好與⊙O相切于點A1，則tan∠A1EF的值為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC中，AB=AC，以AB為直徑的⊙O交BC于點D，交AC于點E．
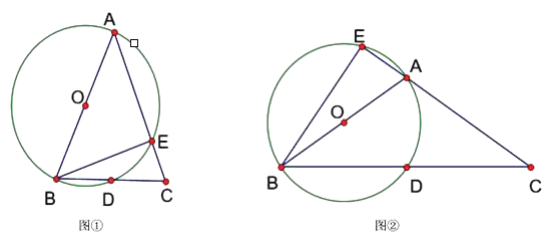
(1)當∠BAC為銳角時，如圖①，求證：∠CBE=
∠BAC；
(2)當∠BAC為鈍角時，如圖②，CA的延長線與⊙O相交于點E，(1)中的結論是否仍然成立？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
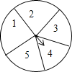
【題目】如圖，有一個可以自由轉動的轉盤，被均勻分成
等份，分別標上
、
、
、
、五個數字．甲乙兩人玩一個游戲，其規則如下：任意轉動轉盤一次，轉盤停止后，指針指向一個數字，如果所得的數字是偶數，則甲勝；如果所得的數字是奇數，則乙勝．
(1)轉出的數字是的概率是________
(2)轉出的數字不大于的概率是________
(3)轉出的數字是偶數的概率是________
(4)你認為這樣的游戲規則對甲、乙兩人是否公平？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】請認真閱讀下面的數學小探究系列，完成所提出的問題：
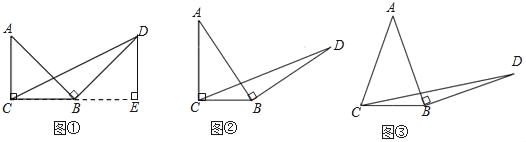
（1）探究1，如圖①，在等腰直角三角形ABC中，∠ACB＝90°，BC＝3，將邊AB繞點B順時針旋轉90°得到線段BD，連接CD，過點D做BC邊上的高DE，則DE與BC的數量關系是 ，△BCD的面積為 ；
（2）探究2，如圖②，在一般的Rt△ABC中，∠ACB＝90°，BC＝a，將邊AB繞點B順時針旋轉90°得到線段BD，連接CD，請用含a的式子表示△BCD的面積，并說明理由；
（3）探究3：如圖③，在等腰三角形ABC中，AB＝AC，BC＝a，將邊AB繞點B順時針旋轉90°得到線段BD，連接CD，試探究用含a的式子表示△BCD的面積，要有探究過程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD中，AB＝6，點E在邊CD上，且CD＝3DE．將△ADE沿AE對折至△AFE，延長EF交邊BC于點G，連接AG、CF．則下列結論：①△ABG≌△AFG②BG＝CG③AG∥CF④S△FGC＝3⑤∠AGB+∠AED＝135°．其中正確的個數是（ ）
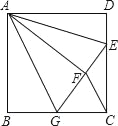
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一元二次方程mx2－2mx＋m－2＝0.
(1)若方程有兩個不等實數根，求m的取值范圍；
(2)若方程的兩實數根為x1，x2，且|x1－x2|＝1，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸、
軸分別交于
、
兩點，拋物線
經過、兩點，與軸的另一個交點為
，連接
．
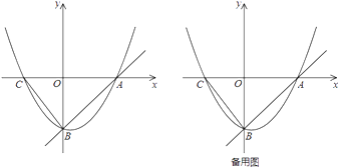
（1）求拋物線的解析式及點的坐標；
（2）點 
在拋物線上，連接 
，當 
時，求點的坐標；
（3）點
從點出發，沿線段
由向運動，同時點
從點出發，沿線段由向運動， 、的運動速度都是每秒
個單位長度，當點到達點時，、同時停止運動，試問在坐標平面內是否存在點
，使、運動過程中的某一時刻，以、、、為頂點的四邊形為菱形？若存在，直接寫出點的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知有一塊等腰三角形紙板，在它的兩腰上各有一點E和F，把這兩點分別與底邊中點連結，并沿著這兩條線段剪下兩個三角形，所得的這兩個三角形相似，剩余部分（四邊形）的四條邊的長度如圖所示，那么原等腰三角形的底邊長為（ ）
A. 
B. 
C. 
或
D. 
或
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com