
【題目】如圖 1,在△ ABC中,∠ACB = 2∠B, ∠BAC的平分線AO交BC于點(diǎn)D,點(diǎn)H為AO上一動(dòng)點(diǎn),過點(diǎn)H作直線l⊥ AO于H,分別交直線AB、AC、BC于點(diǎn)N、E、M
(1)當(dāng)直線l經(jīng)過點(diǎn)C時(shí)(如圖 2),求證:NH = CH;
(2)當(dāng)M是BC中點(diǎn)時(shí),寫出CE和CD之間的等量關(guān)系,并加以證明;
(3)請(qǐng)直接寫出BN、CE、CD之間的等量關(guān)系.



【答案】(1)見解析;(2)CD=2CE,理由見解析;(3)①當(dāng)點(diǎn)M在線段BC上時(shí),CD=BN+CE;
②當(dāng)點(diǎn)M在線段BC的延長線時(shí),CD=BN-CE;③當(dāng)點(diǎn)M在線段CB的延長線上時(shí),CD=CE-BN
【解析】
(1)根據(jù)AD平分∠BAC和CN⊥AD可證△AHC≌△AHN,從而可以得到答案;
(2)過點(diǎn)C作![]() 交AB于點(diǎn)
交AB于點(diǎn)![]() , 過點(diǎn)C作CG∥AB交直線l于點(diǎn)G,結(jié)合(1)再證△BNM≌△CGM即可;
, 過點(diǎn)C作CG∥AB交直線l于點(diǎn)G,結(jié)合(1)再證△BNM≌△CGM即可;
(3)結(jié)合(2)的證明過程,很容易判斷BN、CE、CD之間的等量關(guān)系要分三種情況討論:當(dāng)點(diǎn)M在線段BC上時(shí);當(dāng)點(diǎn)M在線段BC的延長線時(shí);當(dāng)點(diǎn)M在線段CB的延長線上時(shí).
證明:(1)∵AD平分∠BAC
∴∠BAD=∠CAD
∵CN⊥AD
∴∠AHC=∠AHN=90°
∵AH=AH
∴△AHC≌△AHN(ASA)
∴CH=NH
(2)

當(dāng)M是BC中點(diǎn)時(shí),CE和CD的等量關(guān)系為CD=2CE,
理由:證明:過點(diǎn)C作![]() 交AB于點(diǎn)
交AB于點(diǎn)![]() ,
,
連接![]() ,由(1)可知AO是
,由(1)可知AO是![]() 的中垂線,
的中垂線,
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
同理(1)可知△ANH≌AEH(ASA)
∴AN=AE,∠3=∠4
∴![]()
即![]() ,
,
過點(diǎn)C作CG∥AB交直線l于點(diǎn)G,
則∠4=∠2,∠B=∠1
∴∠2=∠3
∴CG=CE,
∵M(jìn)是BC的中點(diǎn),
∴BM=CM
在△BNM和△CGM中,

∴△BNM≌△CGM(ASA)
∴BN=CG,
又∵CG=CE,
∴BN=CE,
∴![]() ;
;
(3)

結(jié)合(2)可知BN、CE、CD之間的等量關(guān)系:
當(dāng)點(diǎn)M在線段BC上時(shí),CD=BN+CE;
當(dāng)點(diǎn)M在線段BC的延長線時(shí),CD=BN-CE;
當(dāng)點(diǎn)M在線段CB的延長線上時(shí),CD=CE-BN.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
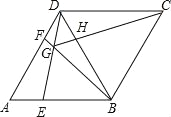
【題目】如圖,在菱形ABCD中,AB=BD,點(diǎn)E、F分別是AB、AD上任意的點(diǎn)(不與端點(diǎn)重合),且AE=DF,連接BF與DE相交于點(diǎn)G,連接CG與BD相交于點(diǎn)H.給出如下幾個(gè)結(jié)論:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,則BG=6GF;④CG與BD一定不垂直;⑤∠BGE=60°.其中正確的結(jié)論個(gè)數(shù)為( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 的平分線交于點(diǎn)
的平分線交于點(diǎn)![]() .
.

(1)求證:![]() ;
;
(2)若![]() 的外角平分線以及
的外角平分線以及![]() 的平分線交于點(diǎn)
的平分線交于點(diǎn)![]() ,(1)結(jié)論是否成立?請(qǐng)?jiān)趫D中補(bǔ)全圖形,寫出結(jié)論,并說明理由.
,(1)結(jié)論是否成立?請(qǐng)?jiān)趫D中補(bǔ)全圖形,寫出結(jié)論,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ ABC中,AB = AC

(1)如圖 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,則∠EDC =
(2)如圖 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,則∠EDC =
(3)思考:通過以上兩題,你發(fā)現(xiàn)∠BAD與∠EDC之間有什么關(guān)系?請(qǐng)用式子表示:
(4)如圖 3,如果AD不是BC上的高,AD = AE,是否仍有上述關(guān)系?如有,請(qǐng)你寫出來,并說明理由
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
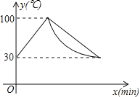
【題目】飲水機(jī)接通電源就進(jìn)入自動(dòng)程序,若在水溫為![]() 時(shí),接通電源后,水溫
時(shí),接通電源后,水溫![]() 和時(shí)間
和時(shí)間![]() 的關(guān)系如圖.開機(jī)加熱時(shí)每分鐘上升
的關(guān)系如圖.開機(jī)加熱時(shí)每分鐘上升![]() ,加熱到
,加熱到![]() ,飲水機(jī)關(guān)機(jī)停止加熱,水溫開始下降,下降時(shí)水溫與開機(jī)后的時(shí)間成反比例關(guān)系.當(dāng)水溫降至
,飲水機(jī)關(guān)機(jī)停止加熱,水溫開始下降,下降時(shí)水溫與開機(jī)后的時(shí)間成反比例關(guān)系.當(dāng)水溫降至![]() ,飲水機(jī)自動(dòng)開機(jī),重復(fù)上述自動(dòng)程序.若上午
,飲水機(jī)自動(dòng)開機(jī),重復(fù)上述自動(dòng)程序.若上午![]() 開機(jī),則
開機(jī),則![]() 時(shí)能否喝到超過
時(shí)能否喝到超過![]() 的水?說明理由.
的水?說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
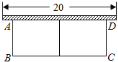
【題目】如圖,有長為![]() 的籬笆,一面利用墻(墻的最大可用長度為
的籬笆,一面利用墻(墻的最大可用長度為![]() ),圍成中間隔有一道籬笆(平行于
),圍成中間隔有一道籬笆(平行于![]() )的矩形花圃
)的矩形花圃![]() .設(shè)花圃的一邊
.設(shè)花圃的一邊![]() 為
為![]() .
.
![]() 則
則![]() ________(用含
________(用含![]() 的代數(shù)式表示),矩形
的代數(shù)式表示),矩形![]() 的面積
的面積![]() ________(用含
________(用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
![]() 如果要圍成面積為
如果要圍成面積為![]() 的花圃,
的花圃,![]() 的長是多少?
的長是多少?
![]() 將
將![]() 中表示矩形
中表示矩形![]() 的面積的代數(shù)式通過配方,問:當(dāng)
的面積的代數(shù)式通過配方,問:當(dāng)![]() 等于多少時(shí),能夠使矩形花圃
等于多少時(shí),能夠使矩形花圃![]() 面積最大,最大的面積為多少?
面積最大,最大的面積為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求證:無論m取何值,原方程總有兩個(gè)不相等的實(shí)數(shù)根;
(2)若x1,x2是原方程的兩根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線y=ax2+bx+c過點(diǎn)A(0,2).
(1)若點(diǎn)(﹣![]() ,0)也在該拋物線上,求a,b滿足的關(guān)系式;
,0)也在該拋物線上,求a,b滿足的關(guān)系式;
(2)若該拋物線上任意不同兩點(diǎn)M(x1,y1),N(x2,y2)都滿足:當(dāng)x1<x2<0時(shí),(x1﹣x2)(y1﹣y2)>0;當(dāng)0<x1<x2時(shí),(x1﹣x2)(y1﹣y2)<0.以原點(diǎn)O為心,OA為半徑的圓與拋物線的另兩個(gè)交點(diǎn)為B,C,且△ABC有一個(gè)內(nèi)角為60°.
①求拋物線的解析式;
②若點(diǎn)P與點(diǎn)O關(guān)于點(diǎn)A對(duì)稱,且O,M,N三點(diǎn)共線,求證:PA平分∠MPN.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AD是△ABC的中線,E、F分別是AD和AD延長線上的點(diǎn),且DE=DF,連結(jié)BF,CE.下列說法:①△ABD和△ACD面積相等;②CE=AE;③△BDF≌△CDE; ④BF∥CE;⑤∠BAD=∠CAD.其中正確的有( ).

A.①⑤B.③⑤C.①③④D.①②④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com