
(1)如圖①,若BC=6,AC=4,∠C=60°,求△ABC的面積S△ABC ;
(2)如圖②,若BC=a,AC=b,∠C=α,求△ABC的面積S△ABC ;
(3)如圖③,四邊形ABCD,若AC=m,BD=n,對角線AC、BD交于O點,它們所成
的銳角為β.求四邊形ABCD的面積S四邊形ABCD .
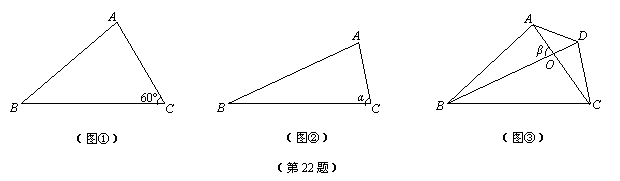
(1)如圖①,過點A作AH⊥BC,垂足為H.
在Rt△AHC 中,
中,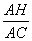 =sin60°,
=sin60°,
∴AH=AC·sin60°=4×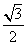 =2
=2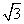 .
.
∴S△ABC= ×BC×AH=
×BC×AH= ×6×2
×6×2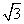 =6
=6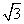 .
.
(2)如圖②,過點A作AH⊥BC,垂足為H.
在Rt△AHC中,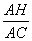 =sinα,
=sinα,
∴AH=AC·sinα=b sinα.
∴S△ABC= ×BC×AH=
×BC×AH= ab sinα
ab sinα
(3)如圖③,分別過點A,C作AH⊥BD,CG⊥BD,垂足為H,G.
在Rt△AHO與Rt△CGO中,AH=OAsinβ,CG=OCsinβ;
于是,S△ABD= ×BD×AH=
×BD×AH= n×OAsinβ;
n×OAsinβ;
S△BCD= ×BD×CG=
×BD×CG= n×OCsinβ;
n×OCsinβ;
∴S四邊形ABCD= S△ABD+S△BCD= n×OAsinβ+
n×OAsinβ+ n×OCsinβ=
n×OCsinβ= n×(OA+OC)sinβ
n×(OA+OC)sinβ
 =
= mnsinβ.
mnsinβ.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
如圖,在平面直角坐標系中,O為坐標原點,點A、B的坐標分別為(0,4)、(-3,0),點E、F分別為AB、BO的中點,分別連接AF、EO,交點為P,點P坐標為
| A.(- | B.(- | C.(-1, | D.(-1,2) |
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
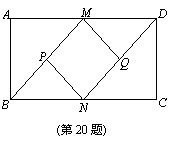
如圖,在矩形ABCD中,M、N分別AD、BC的中點,P、Q分別BM、DN
的中點.
(1)求證:四邊形MPNQ是菱形;
(2)若AB=2,BC=4,求四邊形MPNQ的面積.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
反比例函數y= (k為常數,k≠0)的圖象是雙曲線.當k>0時,雙曲線兩個分支分別在
(k為常數,k≠0)的圖象是雙曲線.當k>0時,雙曲線兩個分支分別在
一、三象限,在每一個象限內,y隨x的增大而減小(簡稱增減性);反比例函數的圖象關于
原點對稱(簡稱對稱性).
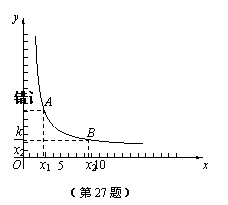 這些我們熟悉的性質,可以通過說理得到嗎?
這些我們熟悉的性質,可以通過說理得到嗎?
【嘗試說理】
我們首先對反比例函數y= (k>0)的增減性來進行說理.
(k>0)的增減性來進行說理.
如圖,當x>0時.
在函數圖象上任意取兩點A、B,設A(x1, ),B(x2,
),B(x2, ),
),
且0<x1< x2.
下面只需要比較 和
和 的大小.
的大小.
 —
— =
=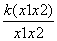 .
.
∵0<x1< x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴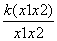 <0.即
<0.即 <
< .
.
這說明:x1< x2時, >
> .也就是:自變量值增大了,對應的函數值反而變小了.
.也就是:自變量值增大了,對應的函數值反而變小了.
即:當x>0時,y隨x的增大而減小.
同理,當x<0時,y隨x的增大而減小.
(1)試說明:反比例函數y=  (k>0)的圖象關于原點對稱.
(k>0)的圖象關于原點對稱.
【運用推廣】
 (2)分別寫出二次函數y=ax2 (a>0,a為常數)的對稱性和增減性,并進行說理.
(2)分別寫出二次函數y=ax2 (a>0,a為常數)的對稱性和增減性,并進行說理.
對稱性: ;
增減性: .
說理:
(3)對于二次函數y=ax2+bx+c (a>0,a,b,c為常數),請你從增減性的角度,簡要解釋為何當x=—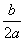 時函數取得最小值.
時函數取得最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com