
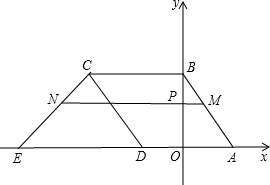
 直線y=-$\frac{4}{3}$x+4與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,菱形ABCD如圖放置在平面直角坐標(biāo)系中,其中點(diǎn)D在x軸負(fù)半軸上,直線y=x+m經(jīng)過點(diǎn)C,交x軸于點(diǎn)E.
直線y=-$\frac{4}{3}$x+4與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,菱形ABCD如圖放置在平面直角坐標(biāo)系中,其中點(diǎn)D在x軸負(fù)半軸上,直線y=x+m經(jīng)過點(diǎn)C,交x軸于點(diǎn)E.分析 (1)由直線的解析式可求出A和B點(diǎn)的坐標(biāo),再根據(jù)菱形的性質(zhì)即可求出點(diǎn)C、點(diǎn)D的坐標(biāo),把點(diǎn)C的坐標(biāo)代入直線y=x+m即可求出m的值;
(2)設(shè)點(diǎn)M的坐標(biāo)為(xM,t),點(diǎn)N的坐標(biāo)為(xN,t),首先求出xM=-$\frac{3}{4}$t+3,再求出xN=t-9,進(jìn)而得到d=xM-xN=-$\frac{3}{2}$t+3-(t-9)=-$\frac{7}{4}$t+12;
(3)先求出點(diǎn)P的坐標(biāo),進(jìn)而得出點(diǎn)P是OB中點(diǎn),即可得出MN是梯形ABCE的中位線即可得出結(jié)論.
解答 解:(1)∵直線y=-$\frac{4}{3}$x+4與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,
∴點(diǎn)A的坐標(biāo)為(3,0)點(diǎn)B的坐標(biāo)為(0,4),
∵四邊形ABCD是菱形,
∵直線y=x+m經(jīng)過點(diǎn)C,
∴m=9,
(2)∵M(jìn)N 經(jīng)過點(diǎn)P(0,t)且平行于x軸,
∴可設(shè)點(diǎn)M的坐標(biāo)為(xM,t),點(diǎn)N的坐標(biāo)為(xN,t),
∵點(diǎn)M在直線AB上,
直線AB的解析式為y=-$\frac{4}{3}$x+4,
∴t=-$\frac{4}{3}$xM+4,得xM=-$\frac{3}{4}$t+3,
同理點(diǎn)N在直線CE上,直線CE的解析式為y=x+9,
∴t=xN+9,得xN=t-9,
∵M(jìn)N∥x軸且線段MN的長度為d,
∴d=xM-xN=-$\frac{3}{4}$t+3-(t-9)=-$\frac{7}{4}$t+12(0≤t≤4)
(3)MN=$\frac{1}{2}$(BC+AE).
理由:當(dāng)t=2時(shí),P(0,2),
∴OP=2,
∵OB=4,
∴點(diǎn)P是OB中點(diǎn),
∵M(jìn)N∥x軸,
∴MN是梯形ABCE的中位線,
∴MN=$\frac{1}{2}$(BC+AE).
點(diǎn)評 此題是一次函數(shù)綜合題,主要考查了菱形的性質(zhì),梯形的中位線,待定系數(shù)法,解本題的關(guān)鍵得出d與t之間的函數(shù)關(guān)系式,是一道比較簡單的中考常考題.


 金版課堂課時(shí)訓(xùn)練系列答案
金版課堂課時(shí)訓(xùn)練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 綜合與探究
綜合與探究查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
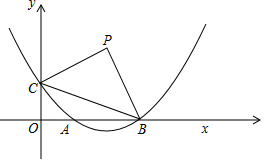 已知:如圖,在平面直角坐標(biāo)系xOy中,拋物線y=ax2-4ax+1與x軸的正半軸交于點(diǎn)A和點(diǎn)B,與y軸交于點(diǎn)C,且OB=3OC,點(diǎn)P是第一象限內(nèi)的點(diǎn),連接BC,△PBC是以BC為斜邊的等腰直角三角形.
已知:如圖,在平面直角坐標(biāo)系xOy中,拋物線y=ax2-4ax+1與x軸的正半軸交于點(diǎn)A和點(diǎn)B,與y軸交于點(diǎn)C,且OB=3OC,點(diǎn)P是第一象限內(nèi)的點(diǎn),連接BC,△PBC是以BC為斜邊的等腰直角三角形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com