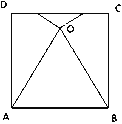
【題目】如圖，將正方形ABCD的邊AD和邊BC折疊，使點C與點D重合于正方形內部一點O，已知點O到邊CD的距離為a，則點O到邊AB的距離為 .（用a的代數式表示）
【答案】（3+2
）a.
【解析】
試題分析：本題考查的是翻轉變換的性質和等邊三角形的性質，翻轉變換是一種對稱變換，它屬于軸對稱，折疊前后圖形的形狀和大小不變，位置變化，對應邊和對應角相等．作OG⊥CD于G，交AB于H，根據翻轉變換的性質得到OA=AD，OB=BC，∠EOA=∠D=90°，∠FOB=∠C=90°，根據直角三角形的性質和勾股定理求出DE、EF、FC，得到正方形的邊長，計算即可．
作OG⊥CD于G，交AB于H，
∵CD∥AB，
∴OH⊥AB于H，
由翻轉變換的性質可知，OA=AD，OB=BC，∠EOA=∠D=90°，∠FOB=∠C=90°，
∴△OAB是等邊三角形，∠EOF=120°，
∴∠OEF=30°，
∴EO=2a，EG=a，
∴DE=OE=2a，OF=FC=2a，EF=2EG=2a，
∴DC=4a+2a，
∴點O到邊AB的距離為4a+2a-a=3a+2a=（3+2）a．
故答案為（3+2）a．
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A的坐標為(3，4)，則A關于x軸對稱的點的坐標是（ ）
A. （－3，4） B. （3，－4） C. （－3，－4） D. （4，3）
查看答案和解析>>
科目：初中數學 來源： 題型：
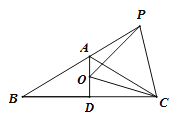
【題目】等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于D，點P是BA延長線上一點，點O是線段AD上一點，OP=OC，以下結論：①∠APO=∠DCO; ②∠APO+∠DCO=30°；③△OPC為等邊三角形；④AC=AD+AP；⑤
. 其中正確的有（ ）
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】△ABC中，AB=AC,∠BAC=120°，點D為AB中點，點E在BC邊上，CE=3BE,AE與CD交于點F, 若AF=
，則FC的長為________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
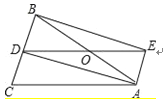
【題目】如圖，△ABC中，AB=AC，AD是∠BAC的角平分線，點O為AB的中點，連接DO并延長到點E，使OE=OD，連接AE，BE．
（1）求證：四邊形AEBD是矩形；
（2）當△ABC滿足什么條件時，矩形AEBD是正方形，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com