
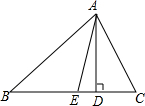
 (1)如圖所示,在△ABC中,AD丄BC于D,AE平分∠BAC,且∠C大于∠B,求證:∠EAD=
(1)如圖所示,在△ABC中,AD丄BC于D,AE平分∠BAC,且∠C大于∠B,求證:∠EAD= (∠C-∠B).
(∠C-∠B). (∠C-∠B).
(∠C-∠B).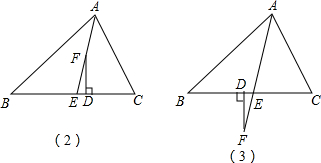 (1)證明:在Rt△ADE中,
(1)證明:在Rt△ADE中, ∠BAC=
∠BAC= (180°-∠C-∠B),
(180°-∠C-∠B), (180°-∠C-∠B)]=
(180°-∠C-∠B)]= (∠C-∠B).
(∠C-∠B). ∠BAC,
∠BAC, ∠BAC+∠EFD=90°;①
∠BAC+∠EFD=90°;① ∠C+
∠C+ ∠B+
∠B+ ∠BAC═90°,②
∠BAC═90°,② (∠C-∠B).
(∠C-∠B). ∠BAC,
∠BAC, ∠BAC+∠EFD=90°;①
∠BAC+∠EFD=90°;① ∠C+
∠C+ ∠B+
∠B+ ∠BAC═90°,②
∠BAC═90°,② (∠C-∠B).
(∠C-∠B). (∠C-∠B).
(∠C-∠B). ∠BAC,所以∠B+
∠BAC,所以∠B+ ∠BAC+∠EFD=90°;聯立△ABC中,由三角形內角和定理得到的式子,即可推出∠EFD,∠B,∠C的關系.
∠BAC+∠EFD=90°;聯立△ABC中,由三角形內角和定理得到的式子,即可推出∠EFD,∠B,∠C的關系. ∠BAC,所以∠B+
∠BAC,所以∠B+ ∠BAC+∠EFD=90°;聯立△ABC中,由三角形內角和定理得到的式子,即可推出∠EFD,∠B,∠C的關系.
∠BAC+∠EFD=90°;聯立△ABC中,由三角形內角和定理得到的式子,即可推出∠EFD,∠B,∠C的關系.

 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
 如圖所示,在離水面高度5米的岸上有人用繩子拉船靠岸,開始時繩子與水平的夾角為30°,此人以每秒0.5米的速度收繩,問:
如圖所示,在離水面高度5米的岸上有人用繩子拉船靠岸,開始時繩子與水平的夾角為30°,此人以每秒0.5米的速度收繩,問:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com