
【題目】如圖,在△ABC中,AB=AC,以AC為直徑作⊙O交BC于點(diǎn)D,過(guò)點(diǎn)D作⊙O的切線,交AB于點(diǎn)E,交CA的延長(zhǎng)線于點(diǎn)F.
(1)求證:EF⊥AB;
(2)若∠C=30°,EF=![]() ,求EB的長(zhǎng).
,求EB的長(zhǎng).

【答案】(1)證明詳見(jiàn)解析;(2)![]() .
.
【解析】
試題分析:(1)連接OD,AD,只要證明OD是△ABC中位線即可解決問(wèn)題.
(2)首先證明AE是△ODF中位線,在Rt△AEF中求出AE,再求出OD,根據(jù)AB=2OD,求出AB即可問(wèn)題.
試題解析:(1)連接OD,AD,
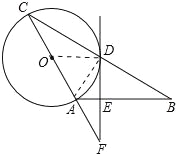
∵AC為⊙O的直徑,
∴∠ADC=90°.
又∵AB=AC,
∴CD=DB.又CO=AO,
∴OD∥AB.
∵FD是⊙O的切線,
∴OD⊥DF.∴FE⊥AB.
(2)∵∠C=30°,
∴∠AOD=60°,
在Rt△ODF中,∠ODF=90°,
∴∠F=30°,
∴OA=OD=![]() OF,
OF,
在Rt△AEF中,∠AEF=90°,∠F=30°
∵EF=![]() ,
,
∴AE=EFtan30°=![]() .
.
∵OD∥AB,OA=OC=AF,
∴OD=2AE=![]() ,AB=2OD=
,AB=2OD=![]() ,
,
∴EB=![]() .
.


 小學(xué)期末沖刺100分系列答案
小學(xué)期末沖刺100分系列答案 期末復(fù)習(xí)檢測(cè)系列答案
期末復(fù)習(xí)檢測(cè)系列答案 超能學(xué)典單元期中期末專(zhuān)題沖刺100分系列答案
超能學(xué)典單元期中期末專(zhuān)題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知△ABC的三個(gè)頂點(diǎn)在格點(diǎn)上.

(1)畫(huà)出△A1B1C1,使它與△ABC關(guān)于直線a對(duì)稱(chēng);
(2)求出△A1B1C1的面積.
(3)在直線a上畫(huà)出點(diǎn)P,使PA+PC最小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算:
(1)25.3+(﹣7.3)+(﹣13.7)+7.3
(2)(1﹣1 ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣24)
)×(﹣24)
(3)33.1﹣10.7﹣(﹣22.9)﹣|﹣ ![]() |
|
(4)29 ![]() ×(﹣12)
×(﹣12)
(5)[﹣22﹣( ![]() ﹣
﹣ ![]() +
+ ![]() )×36]÷5.
)×36]÷5.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形ABCD的每個(gè)頂點(diǎn)上寫(xiě)一個(gè)數(shù),把這個(gè)正方形每條邊的兩端點(diǎn)上的數(shù)加起來(lái),將和寫(xiě)在這條邊上,已知AB上的數(shù)是3,BC上的數(shù)是7,CD上的數(shù)是12,則AD上的數(shù)是( )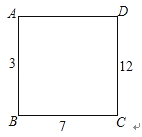
A.2
B.7
C.8
D.15
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
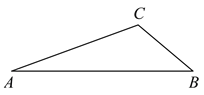
【題目】已知,如圖,在△ABC中,∠C=120°,邊AC的垂直平分線DE與AC、AB分別交于點(diǎn)D和點(diǎn)E.
(1)作出邊AC的垂直平分線DE;
(2)當(dāng)AE=BC時(shí),求∠A的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列圖形,既是軸對(duì)稱(chēng)圖形又是中心對(duì)稱(chēng)圖形的是( )
A. 正三角形B. 正五邊形C. 等腰直角三角形D. 矩形
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知BA⊥AC,CD⊥DB,AC與BD交于O,BD=CA.
求證:⑴ BA=CD; ⑵ △OBC是等腰三角形.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com