
【題目】如圖,在△ABC中,已知點(diǎn)D,E,F分別為BC,AD,AE的中點(diǎn),且S△ABC=4cm2,則陰影部分面積S=( )cm2.
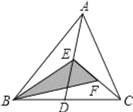
A. 1B. 2C. 3D. 4
【答案】A
【解析】
根據(jù)三角形面積公式由點(diǎn)D為BC的中點(diǎn)得到S△ABD=S△ADC![]() S△ABC=2,同理得到S△EBD=S△EDC
S△ABC=2,同理得到S△EBD=S△EDC![]() S△ABD=1,則S△BEC=2,然后再由點(diǎn)F為EC的中點(diǎn)得到S△BEF
S△ABD=1,則S△BEC=2,然后再由點(diǎn)F為EC的中點(diǎn)得到S△BEF![]() S△BEC=1.
S△BEC=1.
∵點(diǎn)D為BC的中點(diǎn),∴S△ABD=S△ADC![]() S△ABC=2.
S△ABC=2.
∵點(diǎn)E為AD的中點(diǎn),∴S△EBD=S△EDC![]() S△ABD=1,∴S△EBC=S△EBD+S△EDC=2.
S△ABD=1,∴S△EBC=S△EBD+S△EDC=2.
∵點(diǎn)F為EC的中點(diǎn),∴S△BEF![]() S△BEC=1,即陰影部分的面積為1cm2.
S△BEC=1,即陰影部分的面積為1cm2.
故選A.


 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列各組條件中,能夠判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,直線y=-![]() x+3與x軸、y軸相交于A、B兩點(diǎn),點(diǎn)C在線段OA上,將線段CB繞著點(diǎn)C順時針旋轉(zhuǎn)90°得到CD,此時點(diǎn)D恰好落在直線AB上,過點(diǎn)D作DE⊥x軸于點(diǎn)E.
x+3與x軸、y軸相交于A、B兩點(diǎn),點(diǎn)C在線段OA上,將線段CB繞著點(diǎn)C順時針旋轉(zhuǎn)90°得到CD,此時點(diǎn)D恰好落在直線AB上,過點(diǎn)D作DE⊥x軸于點(diǎn)E.
(1)求證:△BOC≌△CED;
(2)如圖2,將△BCD沿x軸正方向平移得△B'C'D',當(dāng)B'C'經(jīng)過點(diǎn)D時,求△BCD平移的距離及點(diǎn)D的坐標(biāo);
(3)若點(diǎn)P在y軸上,點(diǎn)Q在直線AB上,是否存在以C、D、P、Q為頂點(diǎn)的四邊形是平行四邊形?若存在,直接寫出所有滿足條件的P點(diǎn)的坐標(biāo);若不存在,請說明理由.
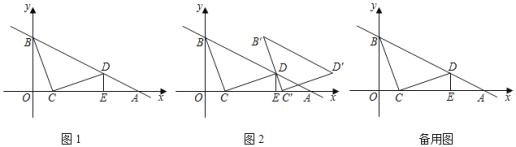
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】 如圖,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
(1)求∠FEC的度數(shù);
(2)若∠BAC=3∠B,求證:AB⊥AC;
(3)當(dāng)∠DAB=______度時,∠BAC=∠AEC.(請直接填出結(jié)果,不用證明)
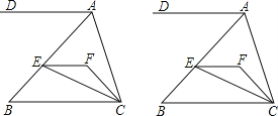
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,Rt△ABC中,∠C=90.
(1)當(dāng)∠B=60時,![]() =_______;當(dāng)∠A=45時,
=_______;當(dāng)∠A=45時,![]() =_______.
=_______.
(2)當(dāng)∠B=2∠A時,求![]() 的值;
的值;
(3)若AB=2BC,求∠A的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,EF∥AB,M,N是線段EF的兩個動點(diǎn),且MN=![]() EF,若把該正方形紙片卷成一個圓柱,使點(diǎn)A與點(diǎn)B重合,若底面圓的直徑為6cm,則正方形紙片上M,N兩點(diǎn)間的距離是____________cm.
EF,若把該正方形紙片卷成一個圓柱,使點(diǎn)A與點(diǎn)B重合,若底面圓的直徑為6cm,則正方形紙片上M,N兩點(diǎn)間的距離是____________cm.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】雅美服裝廠有A種布料70m,B種布料52米.現(xiàn)計劃用這兩種布料生產(chǎn)M、N兩種型號的時裝共80套,已知做一套M型號的時裝共需A種布料0.6m,B種布料0.9m;做一套N型號的時裝需要A種布料1.1m,B種布料0.4m.
(1)設(shè)生產(chǎn)x套M型號的時裝,寫出x應(yīng)滿足的不等式組;
(2)有哪幾種符合題意的生產(chǎn)方案?請你幫助設(shè)計出來.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠B=90°,BC=8 AB=6cm,動點(diǎn)P從點(diǎn)A開始沿邊AB向點(diǎn)B以1cm/s的速度移動,動點(diǎn)Q從點(diǎn)B開始沿邊BC向點(diǎn)C以2cm/s的速度移動.若P,Q兩點(diǎn)分別從A,B兩點(diǎn)同時出發(fā),在運(yùn)動過程中,△PBQ的最大面積是( )
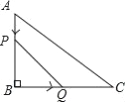
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)![]() 的圖象拋物線與
的圖象拋物線與![]() 軸相交于不同的兩點(diǎn)
軸相交于不同的兩點(diǎn)![]() ,
,![]() ,且
,且![]() ,
,
(1)若拋物線的對稱軸為![]() 求的
求的![]() 值;
值;
(2)若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若該拋物線與![]() 軸相交于點(diǎn)D,連接BD,且∠OBD=60°,拋物線的對稱軸
軸相交于點(diǎn)D,連接BD,且∠OBD=60°,拋物線的對稱軸![]() 與
與![]() 軸相交點(diǎn)E,點(diǎn)F是直線
軸相交點(diǎn)E,點(diǎn)F是直線![]() 上的一點(diǎn),點(diǎn)F的縱坐標(biāo)為
上的一點(diǎn),點(diǎn)F的縱坐標(biāo)為![]() ,連接AF,滿足∠ADB=∠AFE,求該二次函數(shù)的解析式.
,連接AF,滿足∠ADB=∠AFE,求該二次函數(shù)的解析式.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com