
【題目】如圖,![]() 是一張直角三角形彩色紙,
是一張直角三角形彩色紙,![]() ,
,![]() 30
30![]() ,
,![]() 40
40![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() .將斜邊上的高
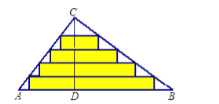
.將斜邊上的高![]() 進(jìn)行五等分,然后裁出4張寬度相等的長方形紙條.則這4張紙條的面積和是______
進(jìn)行五等分,然后裁出4張寬度相等的長方形紙條.則這4張紙條的面積和是______![]() .
.
【答案】480
【解析】
先利用勾股定理計(jì)算出AB=50cm,再利用面積法可計(jì)算出CD=24cm,證明△CEF∽△CAB,由于斜邊上的高CD被五等分,所以![]() 則EF=
則EF=![]() ×50=10,同理可得MN=
×50=10,同理可得MN=![]() AB=20,PQ=
AB=20,PQ=![]() AB=30,GH=
AB=30,GH=![]() AB=40,然后根據(jù)矩形的面積公式計(jì)算.
AB=40,然后根據(jù)矩形的面積公式計(jì)算.
∵∠ACB=90![]() ,AC=30cm,BC=40cm,
,AC=30cm,BC=40cm,
∴AB=![]() =50(cm),
=50(cm),
∵![]() CDAB=
CDAB=![]() ACBC,
ACBC,
∴CD=![]() =24(cm),CK=
=24(cm),CK=![]() (cm)
(cm)
如圖,∵EF∥AB,
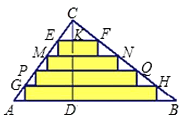
∴△CEF∽△CAB,
∴![]() ,
,
∴EF=![]() ×50=10,
×50=10,
同樣方法可得MN=![]() AB=20,
AB=20,
PQ=![]() AB=30,
AB=30,
GH=![]() AB=40,
AB=40,
∴這4張紙條的面積和=10×![]() +20×
+20×![]() +30×
+30×![]() +40×
+40×![]()
故答案:480.


 全優(yōu)考典單元檢測卷及歸類總復(fù)習(xí)系列答案
全優(yōu)考典單元檢測卷及歸類總復(fù)習(xí)系列答案 品學(xué)雙優(yōu)卷系列答案
品學(xué)雙優(yōu)卷系列答案 小學(xué)期末沖刺100分系列答案
小學(xué)期末沖刺100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
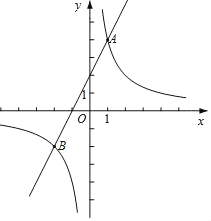
【題目】如圖,在平面直角坐標(biāo)系xOy中,直線y=2x+2與函數(shù)y=![]() (k≠0)的圖象交于A,B兩點(diǎn),且點(diǎn)A的坐標(biāo)為(1,m).
(k≠0)的圖象交于A,B兩點(diǎn),且點(diǎn)A的坐標(biāo)為(1,m).
(1)求k,m的值;
(2)已知點(diǎn)P(a,0),過點(diǎn)P作平行于y軸的直線,交直線y=2x+2于點(diǎn)M,交函數(shù)y=![]() (k≠)的圖象于點(diǎn)N.
(k≠)的圖象于點(diǎn)N.
①當(dāng)a=2時,求線段MN的長;
②若PM>PN,結(jié)合函數(shù)的圖象,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
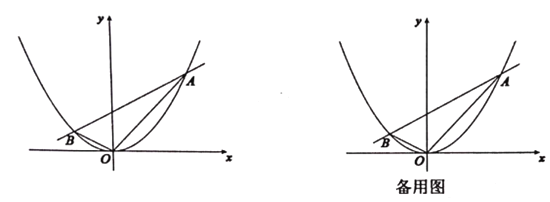
【題目】如圖所示,拋物線![]() 與直線
與直線![]() 交于兩點(diǎn)
交于兩點(diǎn)![]() .已知點(diǎn)
.已知點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]()
(1)求![]() 點(diǎn)坐標(biāo);
點(diǎn)坐標(biāo);
(2)求![]() 的面積;
的面積;
(3)將直線![]() 從原點(diǎn)出發(fā)向上平移
從原點(diǎn)出發(fā)向上平移![]() 個單位,設(shè)
個單位,設(shè)![]() 為直線平移后其上一點(diǎn),且滿足
為直線平移后其上一點(diǎn),且滿足![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
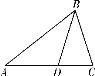
【題目】如圖,在△ABC中,BD是△ABC的角平分線.
(1)尺規(guī)作圖:作BD的垂直平分線分別交AB,BC于點(diǎn)M,N;(保留作圖痕跡,不寫作法)
(2)連接MD,ND,判斷四邊形BMDN的形狀,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中
中![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,作
,作![]() 與
與![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,在
,在![]() 邊上取一點(diǎn)
邊上取一點(diǎn)![]() ,使
,使![]() ,連接
,連接![]() .
.
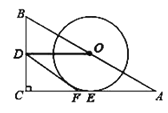
(1)判斷直線![]() 與
與![]() 的位置關(guān)系,并說明理由;
的位置關(guān)系,并說明理由;
(2)當(dāng)![]() ,
,![]() 時,求
時,求![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有兩個一元二次方程![]() ,
,![]() ,其中
,其中![]() ,下列四個結(jié)論中,錯誤的是( )
,下列四個結(jié)論中,錯誤的是( )
A. 如果方程![]() 有兩個不相等的實(shí)數(shù)根,那么方程
有兩個不相等的實(shí)數(shù)根,那么方程![]() 也有兩個不相等的實(shí)數(shù)根
也有兩個不相等的實(shí)數(shù)根
B. ![]() 時,方程
時,方程![]() 和方程
和方程![]() 有一個相同的根,那么這個根必是
有一個相同的根,那么這個根必是![]()
C. 如果![]() 是方程
是方程![]() 的一個根,那么
的一個根,那么![]() 是方程
是方程![]() 的一個根
的一個根
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
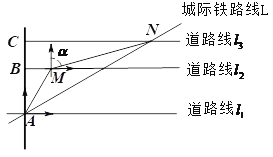
【題目】下圖為某區(qū)域部分交通線路圖,其中直線![]() ,直線
,直線![]() 與直線
與直線![]() 都垂直,,垂足分別為點(diǎn)A、點(diǎn)B和點(diǎn)C,(高速路右側(cè)邊緣),
都垂直,,垂足分別為點(diǎn)A、點(diǎn)B和點(diǎn)C,(高速路右側(cè)邊緣),![]() 上的點(diǎn)M位于點(diǎn)A的北偏東30°方向上,且BM=
上的點(diǎn)M位于點(diǎn)A的北偏東30°方向上,且BM=![]() 千米,
千米,![]() 上的點(diǎn)N位于點(diǎn)M的北偏東
上的點(diǎn)N位于點(diǎn)M的北偏東![]() 方向上,且
方向上,且![]() ,MN=
,MN=![]() 千米,點(diǎn)A和點(diǎn)N是城際線L上的兩個相鄰的站點(diǎn).
千米,點(diǎn)A和點(diǎn)N是城際線L上的兩個相鄰的站點(diǎn).
(1)求![]() 之間的距離
之間的距離
(2)若城際火車平均時速為150千米/小時,求市民小強(qiáng)乘坐城際火車從站點(diǎn)A到站點(diǎn)N需要多少小時?(結(jié)果用分?jǐn)?shù)表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
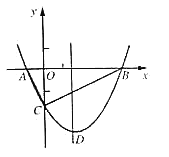
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于
軸交于![]() 點(diǎn),且
點(diǎn),且![]() .
.
(1)求拋物線的解析式及頂點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)判斷![]() 的形狀,證明你的結(jié)論;
的形狀,證明你的結(jié)論;
(3)點(diǎn)![]() 是拋物線對稱軸上的一個動點(diǎn),當(dāng)
是拋物線對稱軸上的一個動點(diǎn),當(dāng)![]() 周長最小時,求點(diǎn)
周長最小時,求點(diǎn)![]() 的坐標(biāo)及
的坐標(biāo)及![]() 的最小周長.
的最小周長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,正方形ABCD的位置如圖所示,點(diǎn)A的坐標(biāo)為(1,0),點(diǎn)D的坐標(biāo)為(0,2)延長CB交x軸于點(diǎn)A1,作正方形A1B1C1C;延長C1B1交x 軸于點(diǎn)A2,作正方形A2B2C2C1,…按這樣的規(guī)律進(jìn)行下去,第2018個正方形的面積為_____.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com