
【題目】若關于![]() 的一元二次方程
的一元二次方程![]() 有兩個實數根,且其中一個根為另一個根的2倍,則稱這樣的方程為“倍根方程”,以下關于倍根方程的說法,正確的是( )
有兩個實數根,且其中一個根為另一個根的2倍,則稱這樣的方程為“倍根方程”,以下關于倍根方程的說法,正確的是( )
①方程![]() 是倍根方程;②若
是倍根方程;②若![]() 是倍根方程,則
是倍根方程,則![]() 或
或![]() ③若點
③若點![]() 在雙曲線
在雙曲線![]() 的圖像上,則關于
的圖像上,則關于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
A. ①B. ①②C. ①③D. ①②③
【答案】D
【解析】
①根據倍根方程定義即可得到方程x2+3x+2=0是倍根方程;②根據倍根方程的定義得到x1,x2,化簡可得結論;③根據已知條件得到pq=2,解方程px2+3x+q=0得到方程的根;
解:①x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1,x2=-2,
∴方程x2+3x+2=0是倍根方程;
故①正確;
②解方程(x-2)(mx-n)=0,
得:x1=2,x2=![]() ,
,
∵(x-2)(mx-n)=0是倍根方程,
∴2=![]() 或4=
或4=![]() ,
,
即m=n或n=4m,
故②正確;
③∵點(p,q)在反比例函數y=![]() 的圖象上,
的圖象上,
∴pq=2,
解方程px2+3x+q=0得:x1=![]() ,x2=
,x2=![]() ,
,
∴x2=2x1,
故③正確;故答案為:①②③.


科目:初中數學 來源: 題型:
【題目】為提高市民的環保意識,某市發出“節能減排,綠色出行”的倡導,某企業抓住機遇投資20萬元購買并投放一批A型“共享單車”,因為單車需求量增加,計劃繼續投放B型單車,B型單車的投放數量與A型單車的投放數量相同,投資總費用減少20%,購買B型單車的單價比購買A型單車的單價少50元,則A型單車每輛車的價格是多少元?設A型單車每輛車的價格為x元,根據題意,列方程正確的是( )
A.![]() =
=![]()
B.![]() =
=![]()
C.![]() =
=![]()
D.![]() =
=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,現給以下結論:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m為實數);⑤4ac﹣b2<0.其中錯誤結論的個數有( )
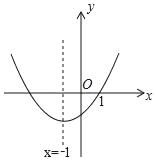
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市購進一批牛肉銷售,經過還價,實際價格每千克比原來少2元,發現原來買這批牛肉32千克的錢,現在可買33千克.
(1)現在實際購進這批牛肉每千克多少元?
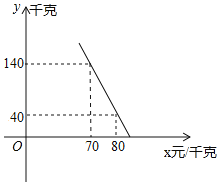
(2)若這批牛肉的銷售量y(千克)與銷售單價x(元/千克)滿足如圖所示的一次函數關系.求y與x之間的函數關系式;
(3)這批牛肉的銷售單價定為多少時,能獲得最大利潤?最大利潤是多少?(利潤=銷售收入﹣進貨金額)
查看答案和解析>>
科目:初中數學 來源: 題型:
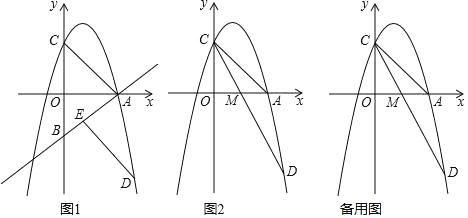
【題目】如圖,在平面直角坐標系中,一次函數y=x﹣3的圖象與x軸交于點A,與y軸交于點B,點B關于x軸的對稱點是C,二次函數y=﹣x2+bx+c的圖象經過點A和點C.
(1)求二次函數的表達式;
(2)如圖1,平移線段AC,點A的對應點D落在二次函數在第四象限的圖象上,點C的對應點E落在直線AB上,求此時點D的坐標;
(3)如圖2,在(2)的條件下,連接CD,交CD軸于點M,點P為直線AC上方拋物線上一動點,過點P作PF⊥AC,垂足為點F,連接PC,是否存在點P,使得以點P,C,F為頂點的三角形與△COM相似?若存在,求點P的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O直徑,AC是⊙O弦,點D是![]() 的中點,弦DE⊥AB,垂足為F,DE交AC于點G.
的中點,弦DE⊥AB,垂足為F,DE交AC于點G.
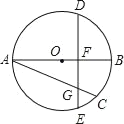
(1)若過點E作⊙O的切線ME,交AC的延長線于點M(請補完整圖形),試問:ME=MG是否成立?若成立,請證明;若不成立,請說明理由;
(2)在滿足第(2)問的條件下,已知AF=3,FB=![]() ,求AG與GM的比.
,求AG與GM的比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C為線段AB上一點,分別以AB、AC、CB為底作頂角為120°的等腰三角形,頂角頂點分別為D、E、F(點E、F在AB的同側,點D在另一側)
(1)如圖1,若點C是AB的中點,則∠AED= ;
(2)如圖2,若點C不是AB的中點
①求證:△DEF為等邊三角形;
②連接CD,若∠ADC=90°,AB=3,請直接寫出EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家客廳里裝有一種三位單極開關,分別控制著A(樓梯)、B(客廳)、C(走廊)三盞電燈,按下任意一個開關均可打開對應的一盞電燈,因剛搬進新房不久,不熟悉情況.
(1)若小明任意按下一個開關,則下列說法正確的是 .
A.小明打開的一定是樓梯燈
B.小明打開的可能是臥室燈
C.小明打開的不可能是客廳燈
D.小明打開走廊燈的概率是![]()
(2)若任意按下一個開關后,再按下另兩個開關中的一個,則正好客廳燈和走廊燈同時亮的概率是多少?請用樹狀圖法或列表法加以說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,動點M、N同時從A點出發,點M沿AB以每秒1個單位長度的速度向中點B運動,點N沿折現ADC以每秒2個單位長度的速度向終點C運動,設運動時間為t秒,則△CMN的面積為S關于t函數的圖象大致是( )

A.  B.
B. 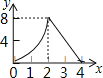
C. 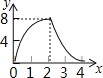 D.
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com