
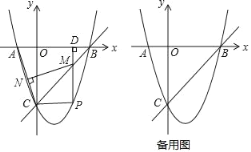
【題目】如圖,已知二次函數(shù)y = ax2 2ax + c圖像的頂點(diǎn)為P,與x軸交于A、B兩點(diǎn)(其中點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,它的對(duì)稱軸交直線BC交于點(diǎn)D,且CD︰BD=1︰2.
(1)求B點(diǎn)坐標(biāo);
(2)當(dāng)△CDP的面積是1時(shí),求二次函數(shù)的表達(dá)式;
(3)若直線BP交y軸于點(diǎn)E,求當(dāng)△CPE是直角三角形時(shí)的a的值.
【答案】(1)B(3,0);(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)當(dāng)![]() 時(shí),由解析式得出對(duì)稱軸方程,得到
時(shí),由解析式得出對(duì)稱軸方程,得到![]() 結(jié)合CD︰BD=1︰2與平行線的性質(zhì)得到答案,同理可得
結(jié)合CD︰BD=1︰2與平行線的性質(zhì)得到答案,同理可得![]() 時(shí)的答案,
時(shí)的答案,
(2)當(dāng)![]() 時(shí),利用△CDP的面積是1,得到
時(shí),利用△CDP的面積是1,得到![]() 利用三角形相似的性質(zhì)表示
利用三角形相似的性質(zhì)表示![]() 的長(zhǎng)度,得到
的長(zhǎng)度,得到![]() 的坐標(biāo),結(jié)合
的坐標(biāo),結(jié)合![]() 的坐標(biāo),用待定系數(shù)法求解即可,同理可得
的坐標(biāo),用待定系數(shù)法求解即可,同理可得![]() 時(shí)的解析式,
時(shí)的解析式,
(3)當(dāng)![]() 時(shí),△CPE是直角三角形時(shí),只有
時(shí),△CPE是直角三角形時(shí),只有![]() 得到
得到![]() 利用勾股定理求解即可,同理可得當(dāng)
利用勾股定理求解即可,同理可得當(dāng)![]() 時(shí)的答案.
時(shí)的答案.
解:(1)如圖,當(dāng)![]() 時(shí),
時(shí),
拋物線的對(duì)稱軸與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,且函數(shù)的對(duì)稱軸是
,且函數(shù)的對(duì)稱軸是![]()
![]()
![]() 軸,
軸,
![]()
![]()
![]()
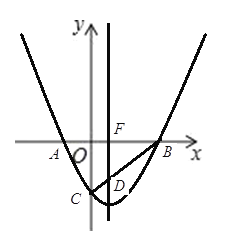
同理:當(dāng)![]() 時(shí),
時(shí),![]()
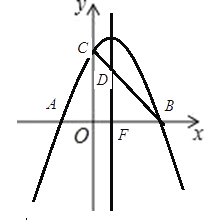
(2)當(dāng)![]() 時(shí),如圖,
時(shí),如圖,![]()
![]()
![]()
![]()
![]() 軸,
軸,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
把![]() 代入解析式得:
代入解析式得:
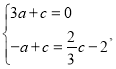
解得:![]()
![]()
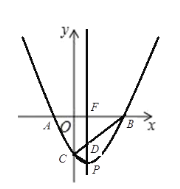
當(dāng)![]() 時(shí),如圖,
時(shí),如圖,
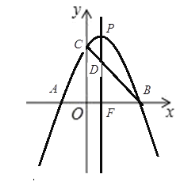
同理可得: ![]()
把![]() 代入
代入![]() ,
,
得;![]()
綜上:![]() 或
或![]()
(3)如圖,把![]() 代入
代入![]() 得:
得:![]()
![]()
當(dāng)![]() 時(shí),
時(shí),
當(dāng)![]() 為直角三角形時(shí),只有
為直角三角形時(shí),只有![]()
則![]()
![]()
![]()
![]()
![]()
![]() (舍去).
(舍去).
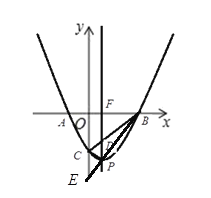
當(dāng)![]() 時(shí),如圖,
時(shí),如圖,
同理可得: 當(dāng)![]() 為直角三角形時(shí),只有
為直角三角形時(shí),只有![]()
則![]()
![]()
![]()
![]()
![]()
![]() (舍去).
(舍去).
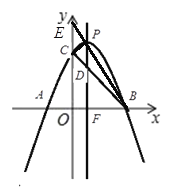
綜上:![]() 或
或![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我市公交總公司為節(jié)約資源同時(shí)惠及民生,擬對(duì)一些乘客數(shù)量較少的路線換成中巴車.該公司計(jì)劃購買![]() 臺(tái)中巴車,現(xiàn)有甲、乙兩種型號(hào),已知購買一臺(tái)甲型車比購買一臺(tái)乙型車少
臺(tái)中巴車,現(xiàn)有甲、乙兩種型號(hào),已知購買一臺(tái)甲型車比購買一臺(tái)乙型車少![]() 萬元,購買
萬元,購買![]() 臺(tái)甲型車比購買
臺(tái)甲型車比購買![]() 臺(tái)乙型車多
臺(tái)乙型車多![]() 萬元.
萬元.
(1)問購買一臺(tái)甲型車和一臺(tái)乙型車分別需要多少萬元?
(2)經(jīng)了解,每臺(tái)甲型車每年節(jié)省費(fèi)用![]() 萬元,每臺(tái)乙型車每年節(jié)省費(fèi)用
萬元,每臺(tái)乙型車每年節(jié)省費(fèi)用![]() 萬元,若要使購買的這批中巴車每年至少能節(jié)省
萬元,若要使購買的這批中巴車每年至少能節(jié)省![]() 萬,則購買甲型車至少多少臺(tái)?
萬,則購買甲型車至少多少臺(tái)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
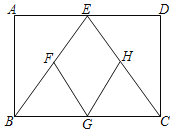
【題目】如圖,已知四邊形ABCD是矩形,點(diǎn)E,G分別是AD,BC邊的中點(diǎn),連接BE,CE,點(diǎn)F,H分別是BE,CE的中點(diǎn)連接FG,HG.
(1)求證:四邊形EFGH是菱形;
(2)當(dāng)![]() = 時(shí),四邊形EFGH是正方形.
= 時(shí),四邊形EFGH是正方形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,在平面直角坐標(biāo)系xOy中,點(diǎn)A的坐標(biāo)為(0,2),點(diǎn)P(m,n)是拋物線![]() 上的一個(gè)動(dòng)點(diǎn).
上的一個(gè)動(dòng)點(diǎn).
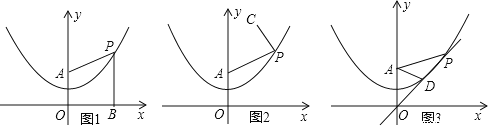
(1)如圖1,過動(dòng)點(diǎn)P作PB⊥x軸,垂足為B,連接PA,請(qǐng)通過測(cè)量或計(jì)算,比較PA與PB的大小關(guān)系:PA_____PB(直接填寫“>”“<”或“=”,不需解題過程);
(2)請(qǐng)利用(1)的結(jié)論解決下列問題:
①如圖2,設(shè)C的坐標(biāo)為(2,5),連接PC,AP+PC是否存在最小值?如果存在,求點(diǎn)P的坐標(biāo);如果不存在,簡(jiǎn)單說明理由;
②如圖3,過動(dòng)點(diǎn)P和原點(diǎn)O作直線交拋物線于另一點(diǎn)D,若AP=2AD,求直線OP的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】《歌手—當(dāng)打之年》是湖南衛(wèi)視最受歡迎的娛樂節(jié)目,奇襲挑戰(zhàn)賽在每周五晚準(zhǔn)時(shí)進(jìn)行,7名主打歌手進(jìn)行比賽的同時(shí)還要接受1名奇襲歌手挑戰(zhàn).近期即將進(jìn)行終極奇襲戰(zhàn),奇襲歌手艾熱將挑戰(zhàn)徐佳瑩(女)、米希亞(女)、蕭敬騰、華晨宇、周深、聲入人心男團(tuán)、旅行團(tuán)樂隊(duì).
(1)當(dāng)主持人詢問艾熱準(zhǔn)備奇襲哪位歌手時(shí),艾熱透露“希望和男性嗓音去比試”,那周深被奇襲的概率是 ;
(2)7名主打歌手比賽的上場(chǎng)順序是通過抽簽方式進(jìn)行,若已經(jīng)知道前4位歌手的上場(chǎng)順序,還有華晨宇、米希亞、周深不知道,那么華晨宇和周深兩位是相鄰出場(chǎng)的概率是多少.(請(qǐng)用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖的![]() 中,
中,![]() ,且
,且![]() 為
為![]() 上一點(diǎn).今打算在
上一點(diǎn).今打算在![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,在
,在![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使得
,使得![]() 與
與![]() 全等,以下是甲、乙兩人的作法:
全等,以下是甲、乙兩人的作法:
(甲)連接![]() ,作
,作![]() 的中垂線分別交
的中垂線分別交![]() 、
、![]() 于
于![]() 點(diǎn)、
點(diǎn)、![]() 點(diǎn),則
點(diǎn),則![]() 、
、![]() 兩點(diǎn)即為所求
兩點(diǎn)即為所求
(乙)過![]() 作與
作與![]() 平行的直線交
平行的直線交![]() 于
于![]() 點(diǎn),過
點(diǎn),過![]() 作與
作與![]() 平行的直線交
平行的直線交![]() 于
于![]() 點(diǎn),則
點(diǎn),則![]() 、
、![]() 兩點(diǎn)即為所求
兩點(diǎn)即為所求
對(duì)于甲、乙兩人的作法,下列判斷何者正確?( )

A. 兩人皆正確B. 兩人皆錯(cuò)誤
C. 甲正確,乙錯(cuò)誤D. 甲錯(cuò)誤,乙正確
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明放學(xué)后從學(xué)校回家,出發(fā)![]() 分鐘時(shí),同桌小強(qiáng)發(fā)現(xiàn)小明的數(shù)學(xué)作業(yè)卷忘記拿了,立即拿著數(shù)學(xué)作業(yè)卷按照同樣的路線去追趕小明,小強(qiáng)出發(fā)
分鐘時(shí),同桌小強(qiáng)發(fā)現(xiàn)小明的數(shù)學(xué)作業(yè)卷忘記拿了,立即拿著數(shù)學(xué)作業(yè)卷按照同樣的路線去追趕小明,小強(qiáng)出發(fā)![]() 分鐘時(shí),小明才想起沒拿數(shù)學(xué)作業(yè)卷,馬上以原速原路返回,在途中與小強(qiáng)相遇.兩人離學(xué)校的路程
分鐘時(shí),小明才想起沒拿數(shù)學(xué)作業(yè)卷,馬上以原速原路返回,在途中與小強(qiáng)相遇.兩人離學(xué)校的路程![]() (米)與小強(qiáng)所用時(shí)間
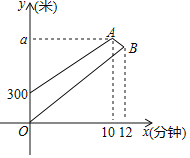
(米)與小強(qiáng)所用時(shí)間![]() (分鐘)之間的函數(shù)圖象如圖所示.
(分鐘)之間的函數(shù)圖象如圖所示.
(1)求函數(shù)圖象中![]() 的值;
的值;
(2)求小強(qiáng)的速度;
(3)求線段![]() 的函數(shù)解析式,并寫出自變量的取值范圍.
的函數(shù)解析式,并寫出自變量的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,將
上,將![]() 沿直線
沿直線![]() 折疊,點(diǎn)
折疊,點(diǎn)![]() 恰好落在
恰好落在![]() 邊上的點(diǎn)
邊上的點(diǎn)![]() 處,且
處,且![]() .
.
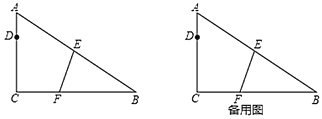
(1)求![]() 的長(zhǎng);
的長(zhǎng);
(2)點(diǎn)![]() 是射線
是射線![]() 上的一個(gè)動(dòng)點(diǎn),連接
上的一個(gè)動(dòng)點(diǎn),連接![]() ,
,![]() ,
,![]() ,
,![]() 的面積與
的面積與![]() 的面積相等,
的面積相等,
①當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),求
上時(shí),求![]() 的長(zhǎng);
的長(zhǎng);
②當(dāng)點(diǎn)![]() 在線段
在線段![]() 的延長(zhǎng)線上時(shí),
的延長(zhǎng)線上時(shí),![]() ________;
________;
(3)將直線![]() 平移,平移后的直線與直線
平移,平移后的直線與直線![]() ,直線
,直線![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() ,以線段
,以線段![]() 為一邊作正方形
為一邊作正方形![]() ,點(diǎn)
,點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 在直線
在直線![]() 兩側(cè),連接
兩側(cè),連接![]() 當(dāng)
當(dāng)![]() 時(shí),請(qǐng)直接寫出
時(shí),請(qǐng)直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y=x2+bx+c交x軸于A,B兩點(diǎn),交y軸于點(diǎn)C,直線y=x﹣3經(jīng)過B,C兩點(diǎn).
(1)求拋物線的解析式;
(2)點(diǎn)P是第四象限內(nèi)拋物線上的動(dòng)點(diǎn),過點(diǎn)P作PD⊥x軸于點(diǎn)D,交直線BC于點(diǎn)M,連接AC,過點(diǎn)M作MN⊥AC于點(diǎn)N,設(shè)點(diǎn)P的橫坐標(biāo)為t.
①求線段MN的長(zhǎng)d與t之間的函數(shù)關(guān)系式(不要求寫出自變量t的取值范圍);
②點(diǎn)Q是平面內(nèi)一點(diǎn),是否存在一點(diǎn)P,使以B,C,P,Q為頂點(diǎn)的四邊形為矩形?若存在,請(qǐng)直接寫出t的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com