【題目】為了創建全國衛生城市，某社區要清理一個衛生死角內的垃圾.若租用甲、乙兩車運送，兩車各運6趟可完成，需支付運費1800元.已知甲、乙兩車單獨運完此堆垃圾，乙車所運的趟數是甲車的1.5倍，且乙車每趟運費比甲車少100元.
（1）求甲、乙兩車單獨運完此堆垃圾各需多少趟？
（2）若單獨租用一臺車，租用哪臺車更合算，請你通過計算說明.
【答案】（1）甲車單獨運完此堆垃圾需10趟，乙車單獨運完此堆垃圾需15趟；（2）若單獨租用一臺車，租用乙車更合算.理由見解析.
【解析】
（1）設定此堆垃圾的量和甲車單獨運完此堆垃圾的趟數，從而可知甲、乙兩車每趟各運送的垃圾量，再根據“若租用甲、乙兩車運送，兩車各運6趟可完成”建立方程求解即可；
（2）先求出甲、乙兩車每趟的運費，再根據“總運費=每趟運費
趟數”求出甲、乙兩車單獨運送所需的總運費，然后比較大小即可得出答案.
（1）設此堆垃圾的量為
，甲車單獨運完此堆垃圾需
趟，則乙車單獨運完此堆垃圾需
趟
因此，甲車每趟運送的垃圾量為
，乙車每趟運送的垃圾量為
由題意得
，即
整理得
解得
經檢驗，是方程的解
則
故甲車單獨運完此堆垃圾需10趟，乙車單獨運完此堆垃圾需15趟；
（2）設甲車每趟運費為
元，則乙車每趟運費為
元
由題意得
整理得
解得
則若單獨租用甲車，所需運費為
（元）
若單獨租用乙車，所需運費為
（元）
因
故若單獨租用一臺車，租用乙車更合算.
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y=ax2+bx+c（a≠0）的圖象如圖，有下列5個結論：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b）（m≠1的實數）．
其中正確結論的有（ ）
A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC與△A1B1C1是位似圖形．
（1）在網格上建立平面直角坐標系，使得點A的坐標為（﹣6，﹣1），點C1的坐標為（﹣3，2），則點B的坐標為 ；
（2）以點A為位似中心，在網格圖中作△AB2C2，使△AB2C2和△ABC位似，且位似比為1：2；
（3）在圖上標出△ABC與△A1B1C1的位似中心P，并寫出點P的坐標為 ，計算四邊形ABCP的周長為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中， ∠B=90°，DE//AB交BC于E、交AC于F，∠CDE=∠ACB=30°，BC=DE．
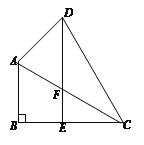
（1）求證：△ACD是等腰三角形；
（2）若AB=4，求CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】操作發現：如圖，已知△ABC和△ADE均為等腰三角形，AB＝AC，AD＝AE，將這兩個三角形放置在一起，使點B，D，E在同一直線上，連接CE．
（1）如圖1，若∠ABC＝∠ACB＝∠ADE＝∠AED＝55°，求證：△BAD≌△CAE；
（2）在（1）的條件下，求∠BEC的度數；
拓廣探索：（3）如圖2，若∠CAB＝∠EAD＝120°，BD＝4，CF為△BCE中BE邊上的高，請直接寫出EF的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，AC與BD相交于點O，AB＝4，BD＝4
，E為AB的中點，點P為線段AC上的動點，則EP+BP的最小值為（ ）
A. 4B. 2
C. 2
D. 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
