
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() (3,0)、
(3,0)、![]() (-1,0).
(-1,0).
(1)求二次函數的解析式;
(2)如圖,二次函數的圖象與![]() 軸交于點
軸交于點![]() ,二次函數圖象的對稱軸與直線
,二次函數圖象的對稱軸與直線![]() 交于點
交于點![]() ,求
,求![]() 點的坐標;
點的坐標;
(3)在第一象限內的拋物線上有一點![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.

【答案】(1)拋物線的解析式為y=-x2+2x+3;(2) P(1,2).(3) Q(![]() ,
, ![]() ).
).
【解析】試題分析:(1)將A、C的坐標代入函數解析式,解方程組求出b、c的值,即可得到函數的解析式;
(2)先令x=0求出B點坐標,然后利用待定系數法求出直線AB的解析式,再在直線AB解析式中令x=1即可得出點P坐標;
(3)設Q(m, ![]() ),△QAB的面積為S,連接QA,QB,OQ,則S=
),△QAB的面積為S,連接QA,QB,OQ,則S=![]() ,用含m的代數式表示S,然后利用二次函數的最值即可求出點Q的坐標.
,用含m的代數式表示S,然后利用二次函數的最值即可求出點Q的坐標.
試題解析:
(1)把點A(3,0)、C(-1,0)代入![]() 中,
中,
得![]() 解得
解得![]()
∴拋物線的解析式為![]() .
.
(2)在![]() 中,當x=0時y=3,
中,當x=0時y=3,
∴B(0,3),
設直線AB的解析式為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直線AB的解析式為![]() ,
,
當x=1時,y=2,
∴P(1,2).
(3)設Q(m, ![]() ),△QAB的面積為S,
),△QAB的面積為S,
連接QA,QB,OQ,則S=![]()
=![]()
又∵![]() ,
,
∴S=![]()
![]()
=![]()
∴當![]() 時S最大,
時S最大,
此時![]() =
=![]() ,
,
∴Q(![]() ,
, ![]() ).
).



 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:初中數學 來源: 題型:
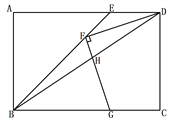
【題目】如圖,矩形ABCD中,BE平分∠ABC交AD于點E,F為BE上一點,連接DF,過F作FG⊥DF交BC于點G,連接BD交FG于點H,若FD = FG, ![]() ,BG = 4,則GH的長為__________.
,BG = 4,則GH的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
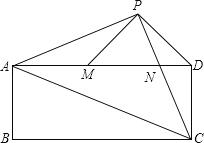
【題目】已知:如圖,在矩形ABCD中,AC是對角線.點P為矩形外一點且滿足AP=PC,AP⊥PC.PC交AD于點N,連接DP,過點P作PM⊥PD交AD于M.
(1)若AP=![]() ,AB=
,AB=![]() BC,求矩形ABCD的面積;
BC,求矩形ABCD的面積;
(2)若CD=PM,求證:AC=AP+PN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學習小組在研究函數y=![]() x3﹣2x的圖象與性質時,已列表、描點并畫出了圖象的一部分.
x3﹣2x的圖象與性質時,已列表、描點并畫出了圖象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)請補全函數圖象;
(2)方程![]() x3﹣2x=﹣2實數根的個數為 ;
x3﹣2x=﹣2實數根的個數為 ;
(3)觀察圖象,寫出該函數的兩條性質.

查看答案和解析>>
科目:初中數學 來源: 題型:
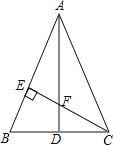
【題目】如圖,△ABC中,AB=AC,作AD⊥BC,CE⊥AB,垂足分別為D,E,AD和CE相交于點F,若已知AE=CE.
(1)求證:△AEF≌△CEB;
(2)求證:AF=2CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABD和∠BDC的平分線交于E,BE交CD于點F,∠1+∠2=90°.

(1)試說明:AB∥CD;
(2)若∠2=25°,求∠BFC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,將三角形CDE繞點C逆時針旋轉75°,點E的對應點N恰好落在OA上,則![]() 的值為( )
的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,D是邊AC上一點,連接BD.將△BCD繞點B逆時針旋轉60°得到△BAE,連接ED.若BC=10,BD=9,求△AED的周長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com