
如圖,將一張等腰直角三角形紙片沿虛線剪成甲、乙、丙三塊,其中甲、丙為直角梯形,乙為等腰直角三角形.根據(jù)圖中標(biāo)示的邊長(zhǎng)數(shù)據(jù),比較甲、乙、丙的面積大小,下列判斷正確的是( )
| A.甲>乙>丙; | B.乙>丙>甲; | C.丙>乙>甲; | D.丙>甲>乙. |
C.
解析試題分析:首先過點(diǎn)B作BH⊥GF于點(diǎn)H,則S乙=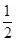 AB•AC,易證得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的長(zhǎng),繼而求得答案.
AB•AC,易證得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的長(zhǎng),繼而求得答案.
如圖:過點(diǎn)B作BH⊥GF于點(diǎn)H,
則S乙=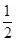 AB•AC,
AB•AC,
∵AC∥DE,
∴△ABC∽△DBE,
∴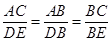 ,
,
∵BC=7,CE=3,
∴DE=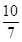 AC,DB=
AC,DB=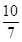 AB,
AB,
∴AD=BD-BA=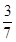 AB,
AB,
∴S丙=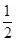 (AC+DE)•AD=
(AC+DE)•AD=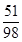 AB•AC,
AB•AC,
∵A∥GF,BH⊥GF,AC⊥AB,
∴BH∥AC,
∴四邊形BDFH是矩形,
∴BH=DF,F(xiàn)H=BD=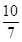 AB,
AB,
∴△GBH∽△BCA,
∴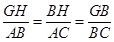 ,
,
∵GB=2,BC=7,
∴GH= AB,BH=
AB,BH= AC,
AC,
∴DF= AC,GF=GH+FH=
AC,GF=GH+FH=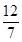 AB,
AB,
∴S甲=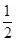 (BD+GF)•DF=
(BD+GF)•DF=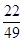 AB•AC,
AB•AC,
∴甲<乙,乙<丙.
故選C.
考點(diǎn): 相似三角形的判定與性質(zhì).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖,鐵路道口的欄桿短臂長(zhǎng)1m,長(zhǎng)臂長(zhǎng)16m.當(dāng)短臂端點(diǎn)下降0.5m時(shí),長(zhǎng)臂端點(diǎn)升高(桿的寬度忽略不計(jì))( )
| A.4m | B.6m | C.8m | D.12m |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
下列命題中,正確的是( )
| A.如果一條直線截三角形兩邊的延長(zhǎng)線所得的對(duì)應(yīng)線段成比例,那么這條直線一定平行于三角形的第三邊; |
| B.不同向量的單位向量的長(zhǎng)度都相等,方向也都相同; |
| C.相似三角形的中線的比等于相似比; |
| D.一般來說,一條線段的黃金分割點(diǎn)有兩個(gè). |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖,DE是△ABC的中位線,延長(zhǎng)DE至F使EF=DE,連接CF,則S△CEF:S四邊形BCED的值為
| A.1∶3 | B.2∶3 | C.1∶4 | D.2∶5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
已知:如圖,在半徑為4的⊙O中,AB為直徑,以弦 (非直徑)為對(duì)稱軸將
(非直徑)為對(duì)稱軸將 折疊后與
折疊后與 相交于點(diǎn)
相交于點(diǎn) ,如果
,如果 ,那么
,那么 的長(zhǎng)為
的長(zhǎng)為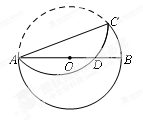
A. | B. | C. | D. |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
下列各組中的四條線段成比例的是( )
| A.4cm、2cm、1cm、3cm | B.1cm、2cm、3cm、5cm |
| C.3cm、4cm、5cm、6cm | D.1cm、2cm、2cm、4cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖,在等邊△ 中,
中, ,當(dāng)直角三角板
,當(dāng)直角三角板 的
的 角的頂點(diǎn)
角的頂點(diǎn) 在
在 上移動(dòng)時(shí),斜邊
上移動(dòng)時(shí),斜邊 始終經(jīng)過
始終經(jīng)過 邊的中點(diǎn)
邊的中點(diǎn) ,設(shè)直角三角板的另一直角邊
,設(shè)直角三角板的另一直角邊 與
與 相交于點(diǎn)E.設(shè)
相交于點(diǎn)E.設(shè)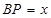 ,
, ,那么
,那么 與
與 之間的函數(shù)圖象大致是( )
之間的函數(shù)圖象大致是( )

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖,將矩形紙片ABCD沿EF折疊,使點(diǎn)B與CD的中點(diǎn)重合,若AB=2,BC=3,則△FCB′與△B′DG的面積之比為( )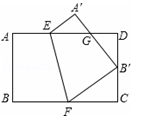
| A.3:2 | B.9:4 | C.4:3 | D.16:9 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com