
【題目】如圖,在![]() 中,
中, ![]() ,
, ![]() 是斜邊上的中線(xiàn),
是斜邊上的中線(xiàn), ![]() 是
是![]() 的中點(diǎn),過(guò)點(diǎn)
的中點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 的延長(zhǎng)線(xiàn)于
的延長(zhǎng)線(xiàn)于![]() ,連接
,連接![]() .
.
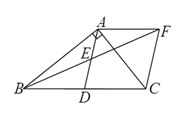
(![]() )求證:
)求證: ![]() .
.
(![]() )判斷四邊形
)判斷四邊形![]() 的形狀,并證明你的結(jié)論.
的形狀,并證明你的結(jié)論.
【答案】(![]() )證明見(jiàn)解析;(
)證明見(jiàn)解析;(![]() )
)![]() 是菱形,證明見(jiàn)解析.
是菱形,證明見(jiàn)解析.
【解析】分析:(1)根據(jù)AAS證△AFE≌△DBE,即可得出結(jié)論;(2)利用(1)中全等三角形的對(duì)應(yīng)邊相等得到AF=BD.結(jié)合已知條件,利用“有一組對(duì)邊平行且相等的四邊形是平行四邊形”得到ADCF是菱形,由“直角三角形斜邊的中線(xiàn)等于斜邊的一半”得到AD=DC,從而得出結(jié)論
本題解析:
(![]() )證明:∵
)證明:∵![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() 是
是![]() 邊上的中線(xiàn),
邊上的中線(xiàn),
∴![]() ,
, ![]() ,
,
在![]() 和
和![]() 中,
中, 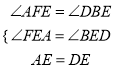 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )四邊形
)四邊形![]() 是菱形,
是菱形,
由(![]() )知,
)知, ![]() ,∵
,∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∵![]() ,
, ![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
∴![]() ,
,
∴四邊形![]() 是菱形.
是菱形.


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案 名師指導(dǎo)一卷通系列答案
名師指導(dǎo)一卷通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)已知等式x-3=5,兩邊同時(shí)________,得x=________,根據(jù)是________;
(2)已知等式4x=3x+7,兩邊同時(shí)________,得x=________,根據(jù)是________;
(3)已知等式![]() ,兩邊同時(shí)________,得x=________,根據(jù)是________.
,兩邊同時(shí)________,得x=________,根據(jù)是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小李從西安通過(guò)某快遞公司給在南昌的外婆寄一盒櫻桃,快遞時(shí),他了解到這個(gè)公司除收取每次6元的包裝費(fèi)外,櫻桃不超過(guò)1kg收費(fèi)22元,超過(guò)1kg,則超出部分按每千克10元加收費(fèi)用.設(shè)該公司從西安到南昌快遞櫻桃的費(fèi)用為y(元),所寄櫻桃為x(kg).
(1)求y與x之間的函數(shù)關(guān)系式;
(2)已知小李給外婆快寄了2.5kg櫻桃,請(qǐng)你求出這次快寄的費(fèi)用是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】因式分解結(jié)果為(x-1)2的多項(xiàng)式是( )
A.x2-2x+1
B.x2+2x+1
C.x2-1
D.x2+1
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】當(dāng)x=1時(shí),代數(shù)式px5+3qx3+4的值為2014,則當(dāng)x=﹣1時(shí),代數(shù)式px5+3qx3+4的值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知三角形的3條中位線(xiàn)分別為3cm、4cm、6cm,則這個(gè)三角形的周長(zhǎng)是( )
A.13cmB.26cmC.24cmD.65cm
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com