
【題目】如圖,已知直線![]() 與拋物線
與拋物線![]() :
:![]() 相交于
相交于![]() 和點
和點![]() 兩點.
兩點.
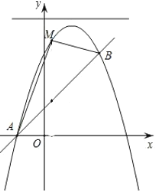
⑴求拋物線![]() 的函數(shù)表達式;
的函數(shù)表達式;
⑵若點![]() 是位于直線
是位于直線![]() 上方拋物線上的一動點,以
上方拋物線上的一動點,以![]() 為相鄰兩邊作平行四邊形
為相鄰兩邊作平行四邊形![]() ,當(dāng)平行四邊形
,當(dāng)平行四邊形![]() 的面積最大時,求此時四邊形
的面積最大時,求此時四邊形![]() 的面積
的面積![]() 及點
及點![]() 的坐標(biāo);
的坐標(biāo);
⑶在拋物線![]() 的對稱軸上是否存在定點
的對稱軸上是否存在定點![]() ,使拋物線
,使拋物線![]() 上任意一點
上任意一點![]() 到點
到點![]() 的距離等于到直線
的距離等于到直線![]() 的距離,若存在,求出定點
的距離,若存在,求出定點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
【答案】⑴![]() ;⑵當(dāng)
;⑵當(dāng)![]() ,
,![]() □MANB=
□MANB=![]() △
△![]() =
=![]() ,此時
,此時![]() ;⑶存在. 當(dāng)
;⑶存在. 當(dāng)![]() 時,無論
時,無論![]() 取任何實數(shù),均有
取任何實數(shù),均有![]() . 理由見解析.
. 理由見解析.
【解析】
(1)利用待定系數(shù)法,將A,B的坐標(biāo)代入y=ax2+2x+c即可求得二次函數(shù)的解析式;
(2)過點M作MH⊥x軸于H,交直線AB于K,求出直線AB的解析式,設(shè)點M(a,-a2+2a+3),則K(a,a+1),利用函數(shù)思想求出MK的最大值,再求出△AMB面積的最大值,可推出此時平行四邊形MANB的面積S及點M的坐標(biāo);
(3)如圖2,分別過點B,C作直線y=![]() 的垂線,垂足為N,H,設(shè)拋物線對稱軸上存在點F,使拋物線C上任意一點P到點F的距離等于到直線y=
的垂線,垂足為N,H,設(shè)拋物線對稱軸上存在點F,使拋物線C上任意一點P到點F的距離等于到直線y=![]() 的距離,其中F(1,a),連接BF,CF,則可根據(jù)BF=BN,CF=CN兩組等量關(guān)系列出關(guān)于a的方程組,解方程組即可.
的距離,其中F(1,a),連接BF,CF,則可根據(jù)BF=BN,CF=CN兩組等量關(guān)系列出關(guān)于a的方程組,解方程組即可.
(1)由題意把點(-1,0)、(2,3)代入y=ax2+2x+c,
得,![]() ,
,
解得a=-1,c=3,
∴此拋物線C函數(shù)表達式為:y=-x2+2x+3;
(2)如圖1,過點M作MH⊥x軸于H,交直線AB于K,
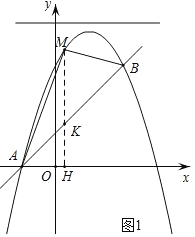
將點(-1,0)、(2,3)代入y=kx+b中,
得,![]() ,
,
解得,k=1,b=1,
∴yAB=x+1,
設(shè)點M(a,-a2+2a+3),則K(a,a+1),
則MK=-a2+2a+3-(a+1)
=-(a-![]() )2+
)2+![]() ,
,
根據(jù)二次函數(shù)的性質(zhì)可知,當(dāng)a=![]() 時,MK有最大長度
時,MK有最大長度![]() ,
,
∴S△AMB最大=S△AMK+S△BMK
=![]() MKAH+
MKAH+![]() MK(xB-xH)
MK(xB-xH)
=![]() MK(xB-xA)
MK(xB-xA)
=![]() ×
×![]() ×3
×3
=![]() ,
,
∴以MA、MB為相鄰的兩邊作平行四邊形MANB,當(dāng)平行四邊形MANB的面積最大時,
S最大=2S△AMB最大=2×![]() =
=![]() ,M(
,M(![]() ,
,![]() );
);
(3)存在點F,
∵y=-x2+2x+3
=-(x-1)2+4,
∴對稱軸為直線x=1,
當(dāng)y=0時,x1=-1,x2=3,
∴拋物線與點x軸正半軸交于點C(3,0),
如圖2,分別過點B,C作直線y=![]() 的垂線,垂足為N,H,
的垂線,垂足為N,H,
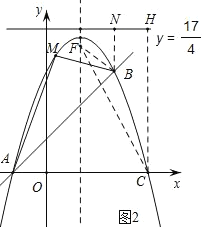
拋物線對稱軸上存在點F,使拋物線C上任意一點P到點F的距離等于到直線y=![]() 的距離,設(shè)F(1,a),連接BF,CF,
的距離,設(shè)F(1,a),連接BF,CF,
則BF=BN=![]() -3=
-3=![]() ,CF=CH=
,CF=CH=![]() ,
,
由題意可列: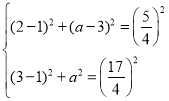 ,
,
解得,a=![]() ,
,
∴F(1,![]() ).
).


 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:初中數(shù)學(xué) 來源: 題型:
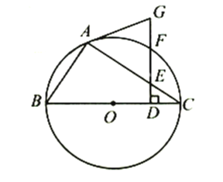
【題目】如圖,![]() 為⊙
為⊙![]() 的內(nèi)接三角形,
的內(nèi)接三角形,![]() 為⊙
為⊙![]() 的直徑,在線段
的直徑,在線段![]() 上取點
上取點![]() (不與端點重合),作
(不與端點重合),作![]() ,分別交
,分別交![]() 、圓周于
、圓周于![]() 、
、![]() ,連接
,連接![]() ,已知
,已知![]() .
.
(1)求證:![]() 為⊙
為⊙![]() 的切線;
的切線;
(2)已知![]() ,填空:
,填空:
①當(dāng)![]() __________
__________![]() 時,四邊形
時,四邊形![]() 是菱形;
是菱形;
②若![]() ,當(dāng)
,當(dāng)![]() __________時,
__________時,![]() 為等腰直角三角形.
為等腰直角三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
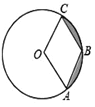
【題目】如圖,已知⊙O的半徑是4,點A,B,C在⊙O上,若四邊形OABC為菱形,則圖中陰影部分面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】圖1是由若干個小圓圈堆成的一個形如等邊三角形的圖案,最上面一層有一個圓圈,以下各層均比上一層多一個圓圈,一共堆了n層.將圖1倒置后與原圖1拼成圖2的形狀,這樣我們可以算出圖1中所有圓圈的個數(shù)為![]() .
.
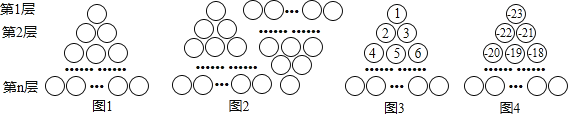
如果圖中的圓圈共有13層,請問:自上往下,在每個圓圈中按圖3的方式填上一串連續(xù)的正整數(shù)1,2,3,4,……,則最底層最左邊這個圓圈中的數(shù)是__________;自上往下,在每個圓圈中按圖4的方式填上一串連續(xù)的整數(shù)﹣23,﹣22,﹣21,﹣20,……,則所有圓圈中各數(shù)的絕對值之和為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
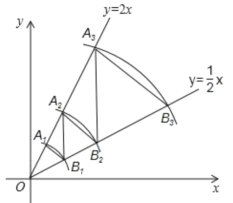
【題目】如圖,在平面直角坐標(biāo)系中,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,以點
,以點![]() 為圓心,以
為圓心,以![]() 長為半徑畫弧,交直線
長為半徑畫弧,交直線![]() 于點
于點![]() ,過
,過![]() 點作
點作![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以
,以![]() 為圓心,以
為圓心,以![]() 長為半徑畫弧,交直線
長為半徑畫弧,交直線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以點
,以點![]() 為圓心,以
為圓心,以![]() 長為半徑畫弧,交直線
長為半徑畫弧,交直線![]() 于點
于點![]() ,過
,過![]() 點作
點作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,以點
,以點![]() 為圓心,以
為圓心,以![]() 長為半徑面弧,交直線
長為半徑面弧,交直線![]() 于點
于點![]() ,…,按照如此規(guī)律進行下去,點
,…,按照如此規(guī)律進行下去,點![]() 的坐標(biāo)為__________.
的坐標(biāo)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線y=ax2+bx+c的對稱軸是直線x=﹣2.拋物線與x軸的一個交點在點(﹣4,0)和點(﹣3,0)之間,其部分圖象如圖所示,下列結(jié)論中正確的個數(shù)有( )①4a﹣b=0;②c≤3a;③關(guān)于x的方程ax2+bx+c=2有兩個不相等實數(shù)根;④b2+2b>4ac.
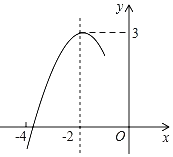
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為4的正方形![]() 中,點
中,點![]() 為對角線
為對角線![]() 上一動點(點
上一動點(點![]() 與點
與點![]() 、
、![]() 不重合),連接
不重合),連接![]() ,作
,作![]() 交射線
交射線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() 、
、![]() ,作射線
,作射線![]() 交射線
交射線![]() 于點
于點![]()
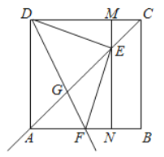
(1)求證:![]() ;
;
(2)當(dāng)![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
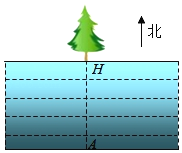
【題目】為了測量一條兩岸平行的河流寬度,三個數(shù)學(xué)研究小組設(shè)計了不同的方案,他們在河南岸的點A處測得河北岸的樹H恰好在A的正北方向.測量方案與數(shù)據(jù)如下表:
課題 | 測量河流寬度 | ||
測量工具 | 測量角度的儀器,皮尺等 | ||
測量小組 | 第一小組 | 第二小組 | 第三小組 |
測量方案示意圖 |
|
|
|
說明 | 點B,C在點A的正東方向 | 點B,D在點A的正東方向 | 點B在點A的正東方向,點C在點A的正西方向. |
測量數(shù)據(jù) | BC=60m, ∠ABH=70°, ∠ACH=35°. | BD=20m, ∠ABH=70°, ∠BCD=35°. | BC=101m, ∠ABH=70°, ∠ACH=35°. |
(1)哪個小組的數(shù)據(jù)無法計算出河寬?
(2)請選擇其中一個方案及其數(shù)據(jù)求出河寬(精確到0.1m).(參考數(shù)據(jù):sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校組建了書法、音樂、美術(shù)、舞蹈、演講5個社團,隨機調(diào)查了部分學(xué)生.被調(diào)查學(xué)生每人都參加且只參加了其中一個社團活動,并將調(diào)查結(jié)果制成了如圖兩幅不完整的統(tǒng)計圖,在扇形統(tǒng)計圖中,“音樂”所對應(yīng)的扇形圓心角度數(shù)是( )度.
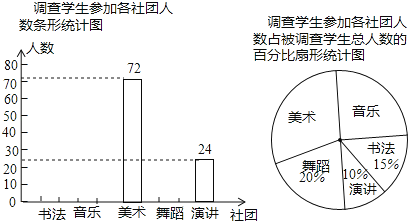
A.25%B.25C.60D.90
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com