【題目】某中學開展“陽光體育一小時”活動，根據學校實際情況，決定開設A：踢毽子；B：籃球；C：跳繩；D：乒乓球四種運動項目.為了解學生最喜歡哪一種運動項目，隨機抽取了一部分學生進行調查，并將調查結果繪制成如下兩個統計圖.請結合圖中的信息解答下列問題：
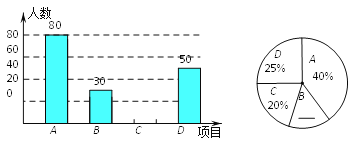
（1）本次共調查了多少名學生？
（2）請將兩個統計圖補充完整.
（3）若該中學有1200名學生，喜歡籃球運動項目的學生約有多少名？
【答案】（1）本次共調查200名學生；
（2）補全圖形見解析；
（3）該學校喜歡乒乓球體育項目的學生約有180人.
【解析】試題分析：（1）結合條形統計圖和扇形統計圖，利用A組頻數80除以A組頻率40%，即可得到該校本次調查中，共調查了多少名學生；（2）利用（1）中所求人數，減去A、B、D組的頻數即可的C組的頻數；B組頻數除以總人數即可得到B組頻率；（3）用1200乘以抽查的人中喜歡籃球運動項目的人數所占的百分比即可．
試題解析：（1）80÷40%=200（人）
∴本次共調查200名學生
（2）200803050=40(人)，
30÷200×100%=15%，
補全如下圖：
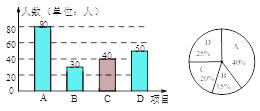
（3）1200×15%=180（人）
∴該學校喜歡乒乓球體育項目的學生約有180人
名校課堂系列答案科目：初中數學 來源： 題型：
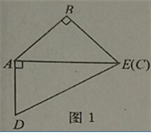
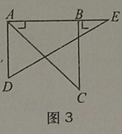
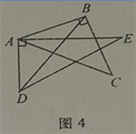
【題目】如圖，取一副三角板按圖1拼接，固定三角板ADE（含30°），將三角板ABC（含45°）繞點A順時針方向旋轉一個大小為α的角（0°＜α≤45°），試問：
（1）當∠α=_____度時，能使圖2中的AB∥DE；
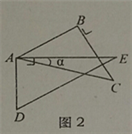
（2）當旋轉到AB與AE重疊時（如圖3），則∠α=_____度；
（3）當△ADE的一邊與△ABC的某一邊平行（不共線）時，直接寫出旋轉角α的所有可能的度數；
（4）當0°＜α≤45°時，連接BD（如圖4），探求∠DBC+∠CAE+∠BDE的值的大小變化情況，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校田徑運動會上，參加男子跳高的16名運動員成績如下表：
成績（m） | 1.45 | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 |
人數 | 3 | 4 | 3 | 2 | 3 | 1 |
則這些運動員成績的中位數是（ ）
A. 1.5B. 1.55C. 1.60D. 1.65
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料并解答問題：
我們知道
的幾何意義是在數軸上數
對應的點與原點的距離： 
，也就是說， 
表示在數軸上數
與數0對應點之間的距離；
這個結論可以推廣為
表示在數軸上數
和數
對應的點之間的距離；
例1解方程
，容易看出，在數軸上與原點距離為2的點對應的數為
，即該方程的解為
．
例2解不等式
，如圖，在數軸上找出
的解，即到1的距離為2的點對應的數為
，3，則
的解集為
或
.
例3解方程
由絕對值的幾何意義知，該方程表示求在數軸上與1和
的距離之和為5的對應的
的值.在數軸上，1和
的距離為3，滿足方程的
對應的點在1的右邊或
的左邊，若
對應的點在1的右邊，由下圖可以看出
；同理，若
對應的點在
的左邊，可得
，故原方程的解是
或
.
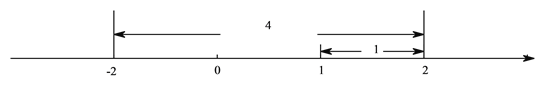
回答問題：（只需直接寫出答案）
①解方程
②解不等式
③解方程
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】關于x的一元二次方程x2+ax﹣1=0的根的情況是（ ）
A. 沒有實數根 B. 只有一個實數根
C. 有兩個相等的實數根 D. 有兩個不相等的實數根
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法不正確的有（ ）個
①從直線外一點到這條直線的垂線段，叫做點到直線的距離②內錯角相等,③過一點有且只有一條直線與已知直線垂直④相等的角是對頂角
A. 0 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com