
【題目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 和
和![]() 上的點(diǎn),且
上的點(diǎn),且![]() .
.
(1)求證:![]()
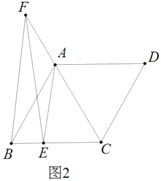
(2)如圖2,![]() 在
在![]() 延長(zhǎng)線上,且
延長(zhǎng)線上,且![]() ,求證:
,求證:![]()
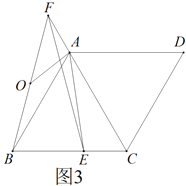
(3)如圖3,在(2)的條件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),求
的中點(diǎn),求![]() 的長(zhǎng).
的長(zhǎng).
【答案】(1)證明見解析;(2)證明見解析;(3)7
【解析】
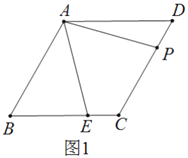
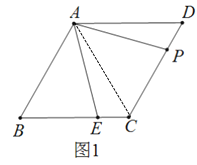
(1)連接AC,如圖1,根據(jù)菱形的性質(zhì)得AB=BC,而∠B=60°,則可判定△ABC為等邊三角形,得到∠BAC=60°,AC=AB,易得∠ACF=60°,∠BAE=∠CAF,然后利用ASA可證明△AEB≌△AFC,即可解答;
(2)過(guò)點(diǎn)F作FH∥AB,交CB的延長(zhǎng)線于點(diǎn)H,利用平行線的性質(zhì)求得△FHC是等邊三角形,得到CF=CH=FH,然后利用AAS定理求得△HBF≌△CEF,從而問(wèn)題得解;
(3)過(guò)點(diǎn)B作BK∥FC,交HF于點(diǎn)K,根據(jù)兩組對(duì)邊分別平行求得四邊形KBAF是平行四邊形,從而求得![]() ,FK=16,過(guò)點(diǎn)A作AM⊥FH,然后利用含30°的直角三角形的性質(zhì)求得MF=
,FK=16,過(guò)點(diǎn)A作AM⊥FH,然后利用含30°的直角三角形的性質(zhì)求得MF=![]() ,
,![]() ,從而求得KM=13,然后利用勾股定理求解即可.
,從而求得KM=13,然后利用勾股定理求解即可.
解:(1)連接AC,如圖1,
∵四邊形ABCD為菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC為等邊三角形,
∴∠BAC=60°,AC=AB,
∴∠BAE+∠EAC=60°,
∵AB∥CD,
∴∠BAC=∠ACP=60°,
∵∠EAP=60°,即∠EAC+∠CAP=60°,
∴∠BAE=∠CAP,
在△AEB和△APC中,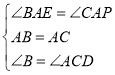 ,
,
∴△AEB≌△APC,
∴BE=CF
∴![]() ;
;
(2)過(guò)點(diǎn)F作FH∥AB,交CB的延長(zhǎng)線于點(diǎn)H
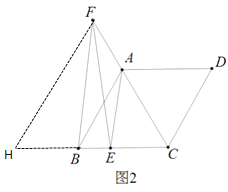
∵FH∥AB
∴∠H=∠CGH=60°
∴△FHC是等邊三角形
∴CF=CH=FH
又∵△ABC是等邊三角形
∴CA=CB
∴AF=BH
又∵FB=FE
∴∠FEB=∠FEB,即∠FBH=∠FEC
在△HBF和△CEF中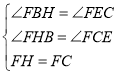
∴△HBF≌△CEF
∴BH=EC
∴AF=EC
(3)過(guò)點(diǎn)B作BK∥FC,交HF于點(diǎn)K,
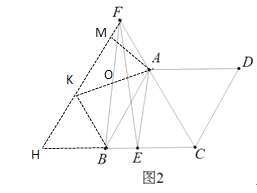
∵BK∥FC,FH∥AB
∴四邊形KBAF是平行四邊形
∴KB=AF=EC=6,![]()
∴FK=AB=BC=BE+EC=BE+AF=16
過(guò)點(diǎn)A作AM⊥FH
由(2)可知,∠CFH=60°
∴在Rt△AMF中,∠MAF=30°
∴MF=![]() ,
,![]()
∴KM=16-3=13
在Rt△AKM中,![]()
∴AO=7.


 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 是等邊三角形,D是BC邊上的一個(gè)動(dòng)點(diǎn)
是等邊三角形,D是BC邊上的一個(gè)動(dòng)點(diǎn)![]() 點(diǎn)D不與B,C重合
點(diǎn)D不與B,C重合![]() 是以AD為邊的等邊三角形,過(guò)點(diǎn)F作BC的平行線交射線AC于點(diǎn)E,連接BF.
是以AD為邊的等邊三角形,過(guò)點(diǎn)F作BC的平行線交射線AC于點(diǎn)E,連接BF.
![]() 如圖1,求證:
如圖1,求證:![]() ≌
≌![]() ;
;
![]() 請(qǐng)判斷圖1中四邊形BCEF的形狀,并說(shuō)明理由;
請(qǐng)判斷圖1中四邊形BCEF的形狀,并說(shuō)明理由;
![]() 若D點(diǎn)在BC邊的延長(zhǎng)線上,如圖2,其它條件不變,請(qǐng)問(wèn)
若D點(diǎn)在BC邊的延長(zhǎng)線上,如圖2,其它條件不變,請(qǐng)問(wèn)![]() 中結(jié)論還成立嗎?如果成立,請(qǐng)說(shuō)明理由.
中結(jié)論還成立嗎?如果成立,請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地震救援隊(duì)探測(cè)出某建筑物廢墟下方點(diǎn)C處有生命跡象,已知廢墟一側(cè)地面上兩探測(cè)點(diǎn)A,B相距3米,探測(cè)線與地面的夾角分別是30°和60°(如圖),試確定生命所在點(diǎn)C的深度.(結(jié)果保留根號(hào))

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為開展全科大閱讀活動(dòng),學(xué)校花費(fèi)了3400元在書店購(gòu)買了40套古典文學(xué)書籍和20套現(xiàn)代文學(xué)書籍,每套現(xiàn)代文學(xué)書籍比每套古典文學(xué)書籍多花20元.
(1)求每套古典文學(xué)習(xí)書籍和現(xiàn)代文學(xué)書籍分別是多少元?
(2)為滿足學(xué)生的閱讀需求,學(xué)校計(jì)劃用不超過(guò)2500元再次購(gòu)買古典文學(xué)和現(xiàn)代文學(xué)書籍共40套,經(jīng)市場(chǎng)調(diào)查得知,每套古典文學(xué)書籍價(jià)格上浮了20%,每套現(xiàn)代文學(xué)書籍價(jià)格下調(diào)了10%,學(xué)校最多能購(gòu)買多少套現(xiàn)代文學(xué)書籍?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】二孩子政策的落實(shí)引起了全社會(huì)的關(guān)注,某校學(xué)生數(shù)學(xué)興趣小組為了了解本校同學(xué)父母生育二孩子的態(tài)度,在學(xué)校抽取了部分同學(xué)對(duì)父母生育二孩子所持的態(tài)度進(jìn)行了問(wèn)卷調(diào)查,調(diào)查分別為非常贊同、贊同、無(wú)所謂、不贊同等四種態(tài)度,現(xiàn)將調(diào)查統(tǒng)計(jì)結(jié)果制成了如圖兩幅統(tǒng)計(jì)圖,請(qǐng)結(jié)合兩幅統(tǒng)計(jì)圖,回答下列問(wèn)題:
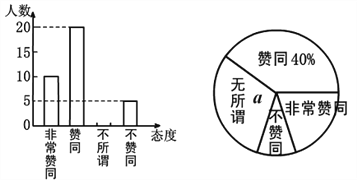
(1)在這次問(wèn)卷調(diào)查中一共抽取了__________名學(xué)生,a=________%;
(2)請(qǐng)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)持“不贊同”態(tài)度的學(xué)生人數(shù)的百分比所占扇形的圓心角為__________度;
(4)若該校有3000名學(xué)生,請(qǐng)你估計(jì)該校學(xué)生對(duì)父母生育二孩子持“贊同”和“非常贊同”兩種態(tài)度的人數(shù)之和.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD是菱形,對(duì)角線AC、BD相交于點(diǎn)O,DH⊥AB于點(diǎn)H,連接OH,∠CAD=35°,則∠HOB的度數(shù)為______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】請(qǐng)認(rèn)真觀察如下圖形:
當(dāng)![]() 時(shí),長(zhǎng)方形
時(shí),長(zhǎng)方形![]() 分為2個(gè)直角三角形;
分為2個(gè)直角三角形;
當(dāng)![]() 時(shí),長(zhǎng)方形
時(shí),長(zhǎng)方形![]() 分為8個(gè)直角三角形;
分為8個(gè)直角三角形;
當(dāng)![]() 時(shí),長(zhǎng)方形
時(shí),長(zhǎng)方形![]() 分為18個(gè)直角三角形;
分為18個(gè)直角三角形;
……

依此規(guī)律,第![]() 個(gè)圖形中,長(zhǎng)方形
個(gè)圖形中,長(zhǎng)方形![]() 被分成______個(gè)小直角三角形.
被分成______個(gè)小直角三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】問(wèn)題再現(xiàn):
數(shù)形結(jié)合是一種重要的數(shù)學(xué)思想方法,借助這種思想方法可將抽象的數(shù)學(xué)知識(shí)變得直觀并且具有可操作性.初中數(shù)學(xué)里的一些代數(shù)公式,很多都可以通過(guò)表示幾何圖形面積的方法進(jìn)行直觀推導(dǎo)和解釋.
例如:利用圖形的幾何意義驗(yàn)證完全平方公式.
將一個(gè)邊長(zhǎng)為![]() 的正方形的邊長(zhǎng)增加
的正方形的邊長(zhǎng)增加![]() ,形成兩個(gè)長(zhǎng)方形和兩個(gè)正方形,如圖所示:這個(gè)圖形的面積可以表示成:
,形成兩個(gè)長(zhǎng)方形和兩個(gè)正方形,如圖所示:這個(gè)圖形的面積可以表示成:
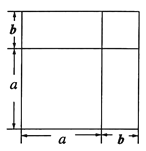
![]() 或
或![]()
∴![]()
這就驗(yàn)證了兩數(shù)和的完全平方公式.
類比解決:
請(qǐng)你類比上述方法,利用圖形的幾何意義驗(yàn)證平方差公式.
(要求畫出圖形并寫出推理過(guò)程)
問(wèn)題提出:如何利用圖形幾何意義的方法證明![]() ?
?
如圖所示,![]() 表示1個(gè)1×1的正方形,即:
表示1個(gè)1×1的正方形,即:![]() ,
,![]() 表示1個(gè)2×2的正方形,
表示1個(gè)2×2的正方形,![]() 與
與![]() 恰好可以拼成1個(gè)2×2的正方形,因此:
恰好可以拼成1個(gè)2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2個(gè)2×2的正方形,即:
就可以表示2個(gè)2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一個(gè)
恰好可以拼成一個(gè)![]() 的大正方形.
的大正方形.
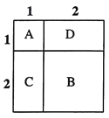
由此可得:![]() .
.
嘗試解決:
請(qǐng)你類比上述推導(dǎo)過(guò)程,利用圖形的幾何意義確定:![]() _______.(要求寫出結(jié)論并構(gòu)造圖形寫出推證過(guò)程).
_______.(要求寫出結(jié)論并構(gòu)造圖形寫出推證過(guò)程).
問(wèn)題拓廣:
請(qǐng)用上面的表示幾何圖形面積的方法探究:![]() _______.(直接寫出結(jié)論即可,不必寫出解題過(guò)程).
_______.(直接寫出結(jié)論即可,不必寫出解題過(guò)程).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com