
【題目】如圖,四邊形![]() ,
,![]() 、
、![]() 分別平分四邊形的外角
分別平分四邊形的外角![]() 和
和![]() ,設(shè)
,設(shè)![]() ,
,![]() .
.
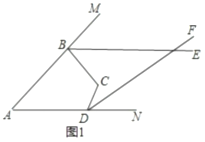
(1)如圖1,若![]() ,求
,求![]() 的度數(shù);
的度數(shù);
(2)如圖1,若![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() ,請寫出
,請寫出![]() 、
、![]() 所滿足的等量關(guān)系式;
所滿足的等量關(guān)系式;
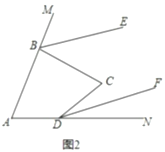
(3)如圖2,若![]() ,判斷
,判斷![]() 、
、![]() 的位置關(guān)系,并說明理由.
的位置關(guān)系,并說明理由.
【答案】(1)120°;(2)![]() ;(3)平行,理由見解析
;(3)平行,理由見解析
【解析】
(1)根據(jù)四邊形的內(nèi)角和可求出∠ABC+∠ADC的度數(shù),利用平角的定義即可得答案;(2)連接BD,根據(jù)角平分線的定義可得∠CBG+∠CDG=![]() (
(![]() ),在△BCD和△BGD中,利用三角形內(nèi)角和定理即可得答案;(3)延長
),在△BCD和△BGD中,利用三角形內(nèi)角和定理即可得答案;(3)延長![]() 交
交![]() 于
于![]() ,根據(jù)角平分線的定義可得∠CBE+∠CDH=
,根據(jù)角平分線的定義可得∠CBE+∠CDH=![]() (
(![]() ),根據(jù)外角性質(zhì)可得
),根據(jù)外角性質(zhì)可得![]() ,即可得出
,即可得出![]() ,根據(jù)
,根據(jù)![]() 可得
可得![]() ,根據(jù)平行線的判定定理即可得BE//DF.
,根據(jù)平行線的判定定理即可得BE//DF.
(1)∵四邊形ABCD的內(nèi)角和為(4-2)×180°=360°,![]()
∴![]() ,
,
∴![]() .
.
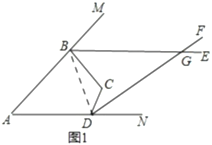
(2)![]()
理由:如圖1,連接![]() ,
,
由(1)得![]() ,
,
∵![]() 、
、![]() 分別平分四邊形的外角
分別平分四邊形的外角![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
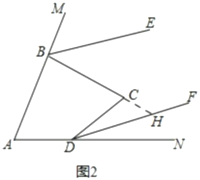
(3)平行,理由如下:
如圖2,延長![]() 交
交![]() 于
于![]() ,
,
由(1)得![]() ,
,
∵![]() 、
、![]() 分別平分四邊形的外角
分別平分四邊形的外角![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在第一個△ABA![]() 中,∠B=20°,AB=A
中,∠B=20°,AB=A![]() B,在A
B,在A![]() B上取一點(diǎn)C,延長AA
B上取一點(diǎn)C,延長AA![]() 到A
到A![]() ,使得A
,使得A![]() A
A![]() =A
=A![]() C,得到第二個△A
C,得到第二個△A![]() A
A![]() C;在A
C;在A![]() C上取一點(diǎn)D,延長A
C上取一點(diǎn)D,延長A![]() A
A![]() 到A
到A![]() ,使得A
,使得A![]() A
A![]() =A
=A![]() D;…,按此做法進(jìn)行下去,則第5個三角形中,以點(diǎn)A4為頂點(diǎn)的底角的度數(shù)為( )
D;…,按此做法進(jìn)行下去,則第5個三角形中,以點(diǎn)A4為頂點(diǎn)的底角的度數(shù)為( )
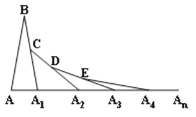
A.5°B.10°C.170°D.175°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店兩次購進(jìn)一批同型號的熱水壺和保溫杯,第一次購進(jìn) 12 個熱水壺和 15 個保溫杯,共用去資金 2850 元,第二次購進(jìn) 20 個熱水壺和 30 個保溫杯,用去資金 4900元(購買同一商品的價格不變)
(1)求每個熱水壺和保溫杯的采購單價各是多少元?
(2)若商場計劃再購進(jìn)同種型號的熱水壺和保溫杯共 80 個,求所需購貨資金 w(元) ,購買熱水壺的數(shù)量 m(個)的函數(shù)表達(dá)式.
(3)在(2)的基礎(chǔ)上,若準(zhǔn)備購買保溫杯的數(shù)量是熱水壺數(shù)量的 3 倍,則該商店需要準(zhǔn)備多少元的購貨資金?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABE中,∠BAE=105°,AE的垂直平分線MN交BE于點(diǎn)C,且AB=CE,則∠B的度數(shù)是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】畫![]() ,使
,使![]() ,
,![]() ,
,![]() 的對邊只能在長度分別為
的對邊只能在長度分別為![]() 、
、![]() 、
、![]() 、
、![]() 的四條線段中任選,可畫出不同形狀的三角形的個數(shù)是( )(提示:在直角三角形中,如果一個銳角等于
的四條線段中任選,可畫出不同形狀的三角形的個數(shù)是( )(提示:在直角三角形中,如果一個銳角等于![]() ,那么它所對的直角邊是斜邊的一半)
,那么它所對的直角邊是斜邊的一半)
A.2個B.3個C.4個D.6個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
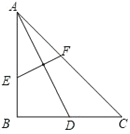
【題目】如圖,已知在△ABC中,∠B=90°,AB=BC,AD是BC邊上的中線,EF是AD的垂直平分線,交AB于點(diǎn)E,交AC于點(diǎn)F,則AE:BE的值為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
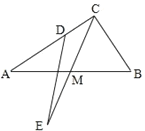
【題目】如圖,已知在Rt△ABC中,∠ACB=90°,M是邊AB的中點(diǎn),連接CM并延長到點(diǎn)E,使得EM=![]() AB,D 是邊AC上一點(diǎn),且AD=BC,連接DE.則∠CDE的度數(shù)為_______.
AB,D 是邊AC上一點(diǎn),且AD=BC,連接DE.則∠CDE的度數(shù)為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,長方形OABC的邊OC=2,將過點(diǎn)B的直線y=x﹣3與x軸交于點(diǎn)E.
(1)求點(diǎn)B的坐標(biāo);
(2)連結(jié)CE,求線段CE的長;
(3)若點(diǎn)P在線段CB上且OP=![]() ,求P點(diǎn)坐標(biāo).
,求P點(diǎn)坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形AOBC中,OB=6,OA=4,分別以O(shè)B,OA所在直線為x軸和y軸,建立如圖所示的平面直角坐標(biāo)系.F是邊BC上一點(diǎn)(不與B、C兩點(diǎn)重合),過點(diǎn)F的反比例函數(shù)y=![]() (k>0)圖象與AC邊交于點(diǎn)E.
(k>0)圖象與AC邊交于點(diǎn)E.

(1)請用k的表示點(diǎn)E,F(xiàn)的坐標(biāo);
(2)若△OEF的面積為9,求反比例函數(shù)的解析式.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com