
若 是關于
是關于 的一元二次方程
的一元二次方程 的兩個根,則方程的兩個根
的兩個根,則方程的兩個根 和系數
和系數 有如下關系:
有如下關系: .
我們把它們稱為根與系數關系定理. 如果設二次函數
.
我們把它們稱為根與系數關系定理. 如果設二次函數 的圖象與x軸的兩個交點為
的圖象與x軸的兩個交點為 .利用根與系數關系定理我們又可以得到A、B兩個交點間的距離為:
.利用根與系數關系定理我們又可以得到A、B兩個交點間的距離為:

請你參考以上定理和結論,解答下列問題:
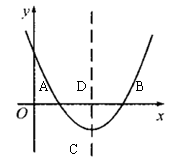
設二次函數 的圖象與x軸的兩個交點為
的圖象與x軸的兩個交點為 ,拋物線的頂點為
,拋物線的頂點為 ,顯然
,顯然 為等腰三角形.
為等腰三角形.
(1)當 為等腰直角三角形時,求
為等腰直角三角形時,求
(2)當 為等邊三角形時,求
為等邊三角形時,求
(1)4(2)12
【解析】⑴ 解:當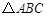 為等腰直角三角形時,過
為等腰直角三角形時,過 作
作 ,垂足為
,垂足為 ,
,
則 ……2分
……2分
∵拋物線與 軸有兩個交點,∴
軸有兩個交點,∴ ,
,
∴ ……4分
……4分
∵
又∵ ,
,
∵ ,
,
∴ ……6分
……6分
∴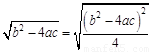
∴
∴ ……9分
……9分
⑵當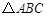 為等邊三角形時,由(1)可知
為等邊三角形時,由(1)可知
CD=  AB……10分
AB……10分
∴  ……11分
……11分
∴b2-4ac=12……12分
(1)由于拋物線與x軸有兩個不同的交點,所以b2-4ac>0;套用材料中的公式可求得線段AB的表達式,利用公式法可得到頂點C的縱坐標,進而求得斜邊AB上的高(設為CD),若△ABC為等腰直角三角形,那么AB=2CD,可根據這個等量關系求出b2-4ac的值.
(2)方法同(1),只不過AB、CD的等量關系為:  AB=2CD.
AB=2CD.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源:2012屆廣東省汕頭市濠江區中考模擬考試數學卷(帶解析) 題型:解答題
若 是關于
是關于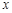 的一元二次方程
的一元二次方程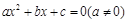 的兩個根,則方程的兩個根
的兩個根,則方程的兩個根 和系數
和系數 有如下關系:
有如下關系: . 我們把它們稱為根與系數關系定理. 如果設二次函數
. 我們把它們稱為根與系數關系定理. 如果設二次函數 的圖象與x軸的兩個交點為
的圖象與x軸的兩個交點為 .利用根與系數關系定理我們又可以得到A、B兩個交點間的距離為:
.利用根與系數關系定理我們又可以得到A、B兩個交點間的距離為:
請你參考以上定理和結論,解答下列問題:
設二次函數 的圖象與x軸的兩個交點為
的圖象與x軸的兩個交點為 ,拋物線的頂點為
,拋物線的頂點為 ,顯然
,顯然 為等腰三角形.
為等腰三角形.
(1)當 為等腰直角三角形時,求
為等腰直角三角形時,求
(2)當 為等邊三角形時,求
為等邊三角形時,求
查看答案和解析>>
科目:初中數學 來源:2013-2014學年浙江省九年級10月月考數學試卷(解析版) 題型:選擇題
若 是關于
是關于 的一元二次方程
的一元二次方程 的一個解,則
的一個解,則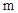 的值是 ( )
的值是 ( )
A.
6 B.  C.
5
D. 2
C.
5
D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com