
【題目】如圖,一次函數(shù)y=kx+b(k≠0)與反比例函數(shù)y= ![]() (m≠0)的圖象有公共點(diǎn)A(1,a)、D(﹣2,﹣1).直線l與x軸垂直于點(diǎn)N(3,0),與一次函數(shù)和反比例函數(shù)的圖象分別交于點(diǎn)B、C.
(m≠0)的圖象有公共點(diǎn)A(1,a)、D(﹣2,﹣1).直線l與x軸垂直于點(diǎn)N(3,0),與一次函數(shù)和反比例函數(shù)的圖象分別交于點(diǎn)B、C.
(1)求一次函數(shù)與反比例函數(shù)的解析式;
(2)根據(jù)圖象回答,x在什么范圍內(nèi),一次函數(shù)的值大于反比例函數(shù)的值;
(3)求△ABC的面積.
【答案】
(1)解:∵反比例函數(shù)經(jīng)過(guò)點(diǎn)D(﹣2,﹣1),
∴把點(diǎn)D代入y= ![]() (m≠0),
(m≠0),
∴﹣1= ![]() ,
,
∴m=2,
∴反比例函數(shù)的解析式為:y= ![]() ,
,
∵點(diǎn)A(1,a)在反比例函數(shù)上,
∴把A代入y= ![]() ,得到a=
,得到a= ![]() =2,
=2,
∴A(1,2),
∵一次函數(shù)經(jīng)過(guò)A(1,2)、D(﹣2,﹣1),
∴把A、D代入y=kx+b (k≠0),得到: ![]() ,解得:
,解得: ![]() ,
,
∴一次函數(shù)的解析式為:y=x+1
(2)解:如圖:當(dāng)﹣2<x<0或x>1時(shí),一次函數(shù)的值大于反比例函數(shù)的值
(3)解:過(guò)點(diǎn)A作AE⊥x軸交x軸于點(diǎn)E,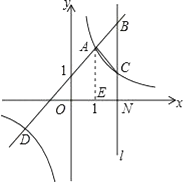
∵直線l⊥x軸,N(3,0),∴設(shè)B(3,p),C(3,q),
∵點(diǎn)B在一次函數(shù)上,∴p=3+1=4,
∵點(diǎn)C在反比例函數(shù)上,∴q= ![]() ,
,
∴S△ABC= ![]() BCEN=
BCEN= ![]() ×(4﹣
×(4﹣ ![]() )×(3﹣1)=
)×(3﹣1)= ![]() .
.
【解析】由反比例函數(shù)經(jīng)過(guò)點(diǎn)D(-2,-1),即可求得反比例函數(shù)的解析式;然后求得點(diǎn)A的坐標(biāo),再利用待定系數(shù)法求得一次函數(shù)的解析式;
結(jié)合圖象求解即可求得x在什么范圍內(nèi),一次函數(shù)的值大于反比例函數(shù)的值;
首先過(guò)點(diǎn)A作AE⊥x軸交x軸于點(diǎn)E,由直線l與x軸垂直于點(diǎn)N(3,0),可求得點(diǎn)E,B,C的坐標(biāo),繼而求得答案.


 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了調(diào)查市場(chǎng)上某品牌方便面的色素含量是否符合國(guó)家標(biāo)準(zhǔn),工作人員在超市里隨機(jī)抽取了某品牌的方便面進(jìn)行檢驗(yàn).圖1和圖2是根據(jù)調(diào)查結(jié)果繪制的兩幅不完整的統(tǒng)計(jì)圖,其中A、B、C、D分別代表色素含量為0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,圖1的條形圖表示的是抽查的方便面中色素含量分布的袋數(shù),圖2的扇形圖表示的是抽查的方便面中色素的各種含量占抽查總數(shù)的百分比.請(qǐng)解答以下問(wèn)題:

(1)本次調(diào)查一共抽查了多少袋方便面?
(2)將圖1中色素含量為B的部分補(bǔ)充完整;
(3)圖2中的色素含量為D的方便面所占的百分比是多少?
(4)若色素含量超過(guò)0.15%即為不合格產(chǎn)品,某超市這種品牌的方便面共有10000袋,那么其中不合格的產(chǎn)品有多少袋?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】圖中折線表示芳芳騎自行車離家的距離與時(shí)間的關(guān)系,她9點(diǎn)離開家,15點(diǎn)回家,請(qǐng)根據(jù)圖象回答下列問(wèn)題:

(1)芳芳到達(dá)離家最遠(yuǎn)的地方時(shí),離家________千米;
(2)第一次休息時(shí)離家________ 千米;
(3)她在10:00~10:30的平均速度是_________;
(4)芳芳一共休息了_________ 小時(shí);
(5)芳芳返回用了____________小時(shí);
(6)返回時(shí)的平均速度是__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,A(a,0),B(0,2![]() )
)
(1)點(diǎn)(k+1,2k﹣5)關(guān)于x軸的對(duì)稱點(diǎn)在第一象限,a為實(shí)數(shù)k的范圍內(nèi)的最大整數(shù),求A點(diǎn)的坐標(biāo)及△AOB的面積;
(2)在(1)的條件下如圖1,點(diǎn)P是第一象限內(nèi)的點(diǎn),且△ABP是以AB為腰的等腰直角三角形,請(qǐng)直接寫出P點(diǎn)坐標(biāo);
(3)在(1)的條件下,如圖2,以AB、OB的作等邊△ABC和等邊△OBD,連接AD、OC交于E點(diǎn),連接BE.
①求證:EB平分∠CED;
②M點(diǎn)是y軸上一動(dòng)點(diǎn),求AM+CM最小時(shí)點(diǎn)M的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于 ![]() 的方程
的方程 ![]() 有兩個(gè)實(shí)數(shù)根
有兩個(gè)實(shí)數(shù)根 ![]() 、
、 ![]() .
.
(1)求實(shí)數(shù)k的取值范圍;
(2)若 ![]() 、
、 ![]() 滿足
滿足 ![]() ,求實(shí)數(shù)
,求實(shí)數(shù) ![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線y=ax2+bx+c的頂點(diǎn)為M(﹣2,﹣4),與x軸交于A、B兩點(diǎn),且A(﹣6,0),與y軸交于點(diǎn)C.
(1)求拋物線的函數(shù)解析式;
(2)求△ABC的面積;
(3)能否在拋物線第三象限的圖象上找到一點(diǎn)P,使△APC的面積最大?若能,請(qǐng)求出點(diǎn)P的坐標(biāo);若不能,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在所給網(wǎng)格圖(每小格均為邊長(zhǎng)是1的正方形)中完成下列各題:(用直尺畫圖)
(1)畫出格點(diǎn)![]() (頂點(diǎn)均在格點(diǎn)上)關(guān)于直線
(頂點(diǎn)均在格點(diǎn)上)關(guān)于直線![]() 對(duì)稱的
對(duì)稱的![]() ;
;
(2)再將![]() 向下平移2單位得
向下平移2單位得![]() ;
;
(3)將![]() 繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°得
繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°得![]() ;并求邊AB掃過(guò)的面積.
;并求邊AB掃過(guò)的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】一次函數(shù)y=-x+1(0≤x≤10)與反比例函數(shù)y= ![]() (-10≤x<0)在同一平面直角坐標(biāo)系中的圖象如圖所示,點(diǎn)(x1 , y1),(x2 , y2)是圖象上兩個(gè)不同的點(diǎn),若y1=y2 , 則x1+x2的取值范圍是( )
(-10≤x<0)在同一平面直角坐標(biāo)系中的圖象如圖所示,點(diǎn)(x1 , y1),(x2 , y2)是圖象上兩個(gè)不同的點(diǎn),若y1=y2 , 則x1+x2的取值范圍是( )
A.- ![]() ≤x≤1
≤x≤1
B.- ![]() ≤x≤
≤x≤ ![]()
C.- ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】【知識(shí)鏈接】 有理化因式:兩個(gè)含有根式的非零代數(shù)式相乘,如果它們的積不含有根式,那么這兩個(gè)代數(shù)式相互叫做有理化因式.
例如: ![]() 的有理化因式是
的有理化因式是 ![]() ;1﹣
;1﹣ ![]() 的有理化因式是1+
的有理化因式是1+ ![]() .
.
分母有理化:分母有理化又稱“有理化分母”,也就是把分母中的根號(hào)化去.指的是如果代數(shù)式中分母有根號(hào),那么通常將分子、分母同乘以分母的有理化因式,達(dá)到化去分母中根號(hào)的目的.如:![]() =
= ![]() =
= ![]() ﹣1,
﹣1, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)【知識(shí)理解】 填空:2 ![]() 的有理化因式是;
的有理化因式是;
直接寫出下列各式分母有理化的結(jié)果:
① ![]() =;②
=;② ![]() = .
= .
(2)【啟發(fā)運(yùn)用】 計(jì)算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com