
【題目】車(chē)間有20名工人,某一天他們生產(chǎn)的零件個(gè)數(shù)統(tǒng)計(jì)如下表:
生產(chǎn)零件的個(gè)數(shù)(個(gè)) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
工人人數(shù)(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求這一天20名工人生產(chǎn)零件的平均個(gè)數(shù);
(2)為了提高大多數(shù)工人的積極性,管理者準(zhǔn)備實(shí)行“每天定額生產(chǎn),超產(chǎn)有獎(jiǎng)”的措施.如果你是管理者,從平均數(shù)、中位數(shù)、眾數(shù)的角度進(jìn)行分析,你將如何確定這個(gè)“定額”?
【答案】(1)這一天20名工人生產(chǎn)零件的平均個(gè)數(shù)為![]() ;(2)中位數(shù)為
;(2)中位數(shù)為![]() ,眾數(shù)為11所以應(yīng)該將定額確定為11個(gè)時(shí),有利于提高大多數(shù)工人的積極性
,眾數(shù)為11所以應(yīng)該將定額確定為11個(gè)時(shí),有利于提高大多數(shù)工人的積極性
【解析】
(1)利用平均數(shù)的定義求解即可;
(2)根據(jù)表中的數(shù)據(jù),求出中位數(shù),眾數(shù),結(jié)合平均數(shù)即可確定 “定額”.
(1)這一天20名工人生產(chǎn)零件的平均個(gè)數(shù)為
![]() ;
;
(2)中位數(shù)為![]() ,眾數(shù)為11
,眾數(shù)為11
當(dāng)定額為12.5時(shí),有8個(gè)人達(dá)標(biāo),8人獲獎(jiǎng),不利于提高大多數(shù)工人的積極性;
當(dāng)定額為12時(shí),有12個(gè)人達(dá)標(biāo),8人獲獎(jiǎng),不利于提高大多數(shù)工人的積極性;
當(dāng)定額為11時(shí),有18個(gè)人達(dá)標(biāo),12人獲獎(jiǎng),有利于提高大多數(shù)工人的積極性;
所以應(yīng)該將定額確定為11個(gè)時(shí),有利于提高大多數(shù)工人的積極性



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
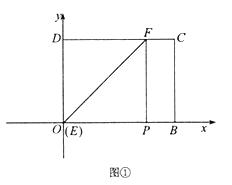
【題目】已知矩形紙片OBCD的邊OB在x軸上,OD在y軸上,點(diǎn)C在第一象限,且![]() .現(xiàn)將紙片折疊,折痕為EF(點(diǎn)E,F是折痕與矩形的邊的交點(diǎn)),點(diǎn)P為點(diǎn)D的對(duì)應(yīng)點(diǎn),再將紙片還原。
.現(xiàn)將紙片折疊,折痕為EF(點(diǎn)E,F是折痕與矩形的邊的交點(diǎn)),點(diǎn)P為點(diǎn)D的對(duì)應(yīng)點(diǎn),再將紙片還原。
(I)若點(diǎn)P落在矩形OBCD的邊OB上,
①如圖①,當(dāng)點(diǎn)E與點(diǎn)O重合時(shí),求點(diǎn)F的坐標(biāo);
②如圖②,當(dāng)點(diǎn)E在OB上,點(diǎn)F在DC上時(shí),EF與DP交于點(diǎn)G,若![]() ,求點(diǎn)F的坐標(biāo):
,求點(diǎn)F的坐標(biāo):
(Ⅱ)若點(diǎn)P落在矩形OBCD的內(nèi)部,且點(diǎn)E,F分別在邊OD,邊DC上,當(dāng)OP取最小值時(shí),求點(diǎn)P的坐標(biāo)(直接寫(xiě)出結(jié)果即可)。

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
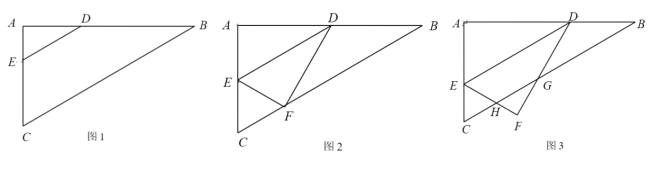
【題目】已知:如圖1,在![]() 中,
中,![]() ,∠ABC=30°,
,∠ABC=30°,![]() ,點(diǎn)
,點(diǎn)![]() 、E分別是邊
、E分別是邊![]() 、AC上動(dòng)點(diǎn),點(diǎn)
、AC上動(dòng)點(diǎn),點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 、
、![]() 重合,DE∥BC.
重合,DE∥BC.
(1)如圖1,當(dāng)AE=1時(shí),求![]() 長(zhǎng);
長(zhǎng);
(2)如圖2,把沿著直線![]() 翻折得到
翻折得到![]() ,設(shè)
,設(shè)![]()
①當(dāng)點(diǎn)F落在斜邊![]() 上時(shí),求
上時(shí),求![]() 的值;
的值;
② 如圖3,當(dāng)點(diǎn)F落在![]() 外部時(shí),EF、DF分別與
外部時(shí),EF、DF分別與![]() 相交于點(diǎn)H、G,如果△ABC和△DEF重疊部分的面積為
相交于點(diǎn)H、G,如果△ABC和△DEF重疊部分的面積為![]() ,求
,求![]() 與
與![]() 的函數(shù)關(guān)系式及定義域.(直接寫(xiě)出答案)
的函數(shù)關(guān)系式及定義域.(直接寫(xiě)出答案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司的午餐采用自助的形式,并倡導(dǎo)員工“適度取餐,減少浪費(fèi)”該公司共有10個(gè)部門(mén),且各部門(mén)的人數(shù)相同.為了解午餐的浪費(fèi)情況,從這10個(gè)部門(mén)中隨機(jī)抽取了![]() 兩個(gè)部門(mén),進(jìn)行了連續(xù)四周(20個(gè)工作日)的調(diào)查,得到這兩個(gè)部門(mén)每天午餐浪費(fèi)飯菜的重量,以下簡(jiǎn)稱(chēng)“每日餐余重量”(單位:千克),并對(duì)這些數(shù)據(jù)進(jìn)行了整理、描述和分析.下面給出了部分信息.
兩個(gè)部門(mén),進(jìn)行了連續(xù)四周(20個(gè)工作日)的調(diào)查,得到這兩個(gè)部門(mén)每天午餐浪費(fèi)飯菜的重量,以下簡(jiǎn)稱(chēng)“每日餐余重量”(單位:千克),并對(duì)這些數(shù)據(jù)進(jìn)行了整理、描述和分析.下面給出了部分信息.![]() .
.![]() 部門(mén)每日餐余重量的頻數(shù)分布直方圖如下(數(shù)據(jù)分成6組:
部門(mén)每日餐余重量的頻數(shù)分布直方圖如下(數(shù)據(jù)分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
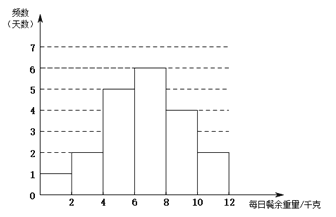
![]() .
.![]() 部門(mén)每日餐余重量在
部門(mén)每日餐余重量在![]() 這一組的是:6.1 6.6 7.0 7.0 7.0 7.8
這一組的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部門(mén)每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部門(mén)每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 兩個(gè)部門(mén)這20個(gè)工作日每日餐余重量的平均數(shù)、中位數(shù)、眾數(shù)如下:
兩個(gè)部門(mén)這20個(gè)工作日每日餐余重量的平均數(shù)、中位數(shù)、眾數(shù)如下:
部門(mén) | 平均數(shù) | 中位數(shù) | 眾數(shù) |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根據(jù)以上信息,回答下列問(wèn)題:
(1)寫(xiě)出表![]() 中的值;
中的值;
(2)在![]() 這兩個(gè)部門(mén)中,“適度取餐,減少浪費(fèi)”做得較好的部門(mén)是________(填“
這兩個(gè)部門(mén)中,“適度取餐,減少浪費(fèi)”做得較好的部門(mén)是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)結(jié)合![]() 這兩個(gè)部門(mén)每日餐余重量的數(shù)據(jù),估計(jì)該公司(10個(gè)部門(mén))一年(按240個(gè)工作日計(jì)算)的餐余總重量.
這兩個(gè)部門(mén)每日餐余重量的數(shù)據(jù),估計(jì)該公司(10個(gè)部門(mén))一年(按240個(gè)工作日計(jì)算)的餐余總重量.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某水果批發(fā)市場(chǎng)香蕉的價(jià)格如下表
購(gòu)買(mǎi)香蕉數(shù)(千克) | 不超過(guò)20千克 | 20千克以上但不超過(guò)40千克 | 40千克以上 |
每千克的價(jià)格 | 6元 | 5元 | 4元 |
張強(qiáng)兩次共購(gòu)買(mǎi)香蕉50千克,已知第二次購(gòu)買(mǎi)的數(shù)量多于第一次購(gòu)買(mǎi)的數(shù)量,共付出264元,請(qǐng)問(wèn)張強(qiáng)第一次,第二次分別購(gòu)買(mǎi)香蕉多少千克?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】若二次函數(shù)![]() 和
和![]() 的圖象關(guān)于原點(diǎn)成中心對(duì)稱(chēng),我們就稱(chēng)其中一個(gè)函數(shù)是另一個(gè)函數(shù)的中心對(duì)稱(chēng)函數(shù),也稱(chēng)函數(shù)
的圖象關(guān)于原點(diǎn)成中心對(duì)稱(chēng),我們就稱(chēng)其中一個(gè)函數(shù)是另一個(gè)函數(shù)的中心對(duì)稱(chēng)函數(shù),也稱(chēng)函數(shù)![]() 和
和![]() 互為中心對(duì)稱(chēng)函數(shù).
互為中心對(duì)稱(chēng)函數(shù).
![]() 求函數(shù)
求函數(shù)![]() 的中心對(duì)稱(chēng)函數(shù);
的中心對(duì)稱(chēng)函數(shù);
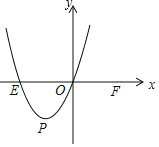
![]() 如圖,在平面直角坐標(biāo)系xOy中,E,F(xiàn)兩點(diǎn)的坐標(biāo)分別為
如圖,在平面直角坐標(biāo)系xOy中,E,F(xiàn)兩點(diǎn)的坐標(biāo)分別為![]() ,
,![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖象經(jīng)過(guò)點(diǎn)E和原點(diǎn)O,頂點(diǎn)為
的圖象經(jīng)過(guò)點(diǎn)E和原點(diǎn)O,頂點(diǎn)為![]() 已知函數(shù)
已知函數(shù)![]() 和
和![]() 互為中心對(duì)稱(chēng)函數(shù);
互為中心對(duì)稱(chēng)函數(shù);
![]() 請(qǐng)?jiān)趫D中作出二次函數(shù)
請(qǐng)?jiān)趫D中作出二次函數(shù)![]() 的頂點(diǎn)
的頂點(diǎn)![]() 作圖工具不限
作圖工具不限![]() ,并畫(huà)出函數(shù)
,并畫(huà)出函數(shù)![]() 的大致圖象;
的大致圖象;
![]() 當(dāng)四邊形EPFQ是矩形時(shí),請(qǐng)求出a的值;
當(dāng)四邊形EPFQ是矩形時(shí),請(qǐng)求出a的值;
![]() 已知二次函數(shù)
已知二次函數(shù)![]() 和
和![]() 互為中心對(duì)稱(chēng)函數(shù),且
互為中心對(duì)稱(chēng)函數(shù),且![]() 的圖象經(jīng)過(guò)
的圖象經(jīng)過(guò)![]() 的頂點(diǎn)當(dāng)
的頂點(diǎn)當(dāng)![]() 時(shí),求代數(shù)式
時(shí),求代數(shù)式![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在等腰![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在
在![]() 上,
上,![]() ,將線段
,將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 按順時(shí)針?lè)较蛐D(zhuǎn)
按順時(shí)針?lè)较蛐D(zhuǎn)![]() 得到
得到![]() ,連接
,連接![]() ,然后把
,然后把![]() 沿著
沿著![]() 翻折得到
翻折得到![]() ,連接
,連接![]() ,
,![]() ,取
,取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,則
,則![]() 的長(zhǎng)為( )
的長(zhǎng)為( )

A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB∥EF,則∠A、∠C、∠D、∠E滿足的數(shù)量關(guān)系是( )
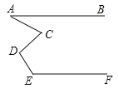
A. ∠A+∠C+∠D+∠E=360°B. ∠A-∠C+∠D+∠E=180°
C. ∠E-∠C+∠D-∠A=90°D. ∠A+∠D=∠C+∠E
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】先閱讀下列材料:
我們已經(jīng)學(xué)過(guò)將一個(gè)多項(xiàng)式分解因式的方法有提公因式法和運(yùn)用公式法,其實(shí)分解因式的方法還有分組分解法、拆項(xiàng)法、十字相乘法等等.
(1)分組分解法:將一個(gè)多項(xiàng)式適當(dāng)分組后,可提公因式或運(yùn)用公式繼續(xù)分解的方法.
如:ax+by+bx+ay=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
2xy+y2﹣1+x2
=x2+2xy+y2﹣1
=(x+y)2﹣1
=(x+y+1)(x+y﹣1)
(2)拆項(xiàng)法:將一個(gè)多項(xiàng)式的某一項(xiàng)拆成兩項(xiàng)后,可提公因式或運(yùn)用公式繼續(xù)分解的方法.如:
x2+2x﹣3
=x2+2x+1﹣4
=(x+1)2﹣22
=(x+1+2)(x+1﹣2)
=(x+3)(x﹣1)
請(qǐng)你仿照以上方法,探索并解決下列問(wèn)題:
(1)分解因式: ![]()
(2)分解因式:x2﹣6x﹣7;
(3)分解因式: ![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com