
已知拋物線:
的頂點在坐標(biāo)軸上.
(1)求的值;
(2)時,拋物線
向下平移
個單位后與拋物線
:
關(guān)于
軸對稱,且
過點
,求
的函數(shù)關(guān)系式;
(3)時,拋物線
的頂點為
,且過點
.問在直線
上是否存在一點
使得△
的周長最小,如果存在,求出點
的坐標(biāo), 如果不存在,請說明理由.
.解:當(dāng)拋物線的頂點在
軸上時
解得或
………………………………1分
當(dāng)拋物線的頂點在
軸上時
∴ ………………………………2分
綜上或
.
(2)當(dāng)時,
拋物線為
.
向下平移個單位后得到
拋物線與拋物線
:
關(guān)于
軸對稱
∴,
,
…………………………………3分
∴拋物線:
∵過點
∴,即
……………………………………4分
解得(由題意
,舍去)∴
∴拋物線:
. ………………………………………………5分
(3)當(dāng)時
拋物線:
頂點
∵過點
∴
∴ ………………6分
作點關(guān)于直線
的對稱點
直線的解析式為
∴ ………………………………………7分
解析:略


 學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案
學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案 小學(xué)課堂作業(yè)系列答案
小學(xué)課堂作業(yè)系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數(shù)學(xué) 來源: 題型:
已知拋物線![]() :
:![]() 的頂點在坐標(biāo)軸上.
的頂點在坐標(biāo)軸上.
(1)求![]() 的值;
的值;
(2)![]() 時,拋物線
時,拋物線![]() 向下平移
向下平移![]() 個單位后與拋物線
個單位后與拋物線![]() :
:![]() 關(guān)于
關(guān)于![]() 軸對稱,且
軸對稱,且![]() 過點
過點![]() ,求
,求![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)![]() 時,拋物線
時,拋物線![]() 的頂點為
的頂點為![]() ,且過點
,且過點![]() .問在直線
.問在直線![]() 上是否存在一點
上是否存在一點![]() 使得△
使得△![]() 的周長最小,如果存在,求出點
的周長最小,如果存在,求出點![]() 的坐標(biāo),如果不存在,請說明理由.
的坐標(biāo),如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011屆北京市石景山區(qū)初中畢業(yè)暨中考一模數(shù)學(xué)試題 題型:解答題
已知拋物線 :
: 的頂點在坐標(biāo)軸上.
的頂點在坐標(biāo)軸上.
(1)求 的值;
的值;
(2) 時,拋物線
時,拋物線 向下平移
向下平移 個單位后與拋物線
個單位后與拋物線 :
: 關(guān)于
關(guān)于 軸對稱,且
軸對稱,且 過點
過點 ,求
,求 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3) 時,拋物線
時,拋物線 的頂點為
的頂點為 ,且過點
,且過點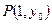 .問在直線
.問在直線 上是否存在一點
上是否存在一點 使得△
使得△ 的周長最小,如果存在,求出點
的周長最小,如果存在,求出點 的坐標(biāo), 如果不存在,請說明理由.
的坐標(biāo), 如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011屆北京市石景山區(qū)中考數(shù)學(xué)一模試卷 題型:解答題
已知拋物線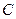 :
: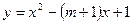 的頂點在坐標(biāo)軸上.
的頂點在坐標(biāo)軸上.
(1)求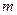 的值;
的值;
(2)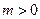 時,拋物線
時,拋物線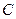 向下平移
向下平移 個單位后與拋物線
個單位后與拋物線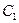 :
: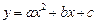 關(guān)于
關(guān)于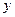 軸對稱,且
軸對稱,且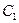 過點
過點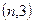 ,求
,求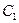 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)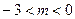 時,拋物線
時,拋物線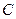 的頂點為
的頂點為 ,且過點
,且過點 .問在直線
.問在直線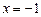 上是否存在一點
上是否存在一點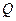 使得△
使得△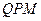 的周長最小,如果存在,求出點
的周長最小,如果存在,求出點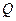 的坐標(biāo), 如果不存在,請說明理由.
的坐標(biāo), 如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2010-2011學(xué)年北京市順義區(qū)初三一模數(shù)學(xué)試題 題型:解答題
已知拋物線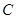 :
: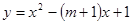 的頂點在坐標(biāo)軸上.
的頂點在坐標(biāo)軸上.
(1)求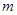 的值;
的值;
(2)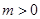 時,拋物線
時,拋物線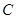 向下平移
向下平移 個單位后與拋物線
個單位后與拋物線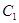 :
: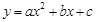 關(guān)于
關(guān)于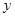 軸對稱,且
軸對稱,且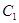 過點
過點 ,求
,求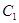 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)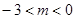 時,拋物線
時,拋物線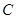 的頂點為
的頂點為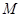 ,且過點
,且過點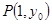 .問在直線
.問在直線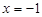 上是否存在一點
上是否存在一點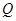 使得△
使得△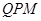 的周長最小,如果存在,求出點
的周長最小,如果存在,求出點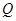 的坐標(biāo), 如果不存在,請說明理由.
的坐標(biāo), 如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2010-2011學(xué)年北京市考數(shù)學(xué)一模試卷 題型:解答題
已知拋物線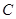 :
: 的頂點在坐標(biāo)軸上.
的頂點在坐標(biāo)軸上.
(1)求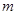 的值;
的值;
(2)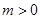 時,拋物線
時,拋物線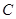 向下平移
向下平移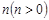 個單位后與拋物線
個單位后與拋物線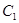 :
: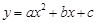 關(guān)于
關(guān)于 軸對稱,且
軸對稱,且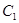 過點
過點 ,求
,求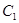 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3) 時,拋物線
時,拋物線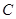 的頂點為
的頂點為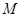 ,且過點
,且過點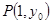 .問在直線
.問在直線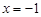 上是否存在一點
上是否存在一點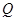 使得△
使得△ 的周長最小,如果存在,求出點
的周長最小,如果存在,求出點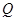 的坐標(biāo),
如果不存在,請說明理由.
的坐標(biāo),
如果不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com