
【題目】如圖, 在三邊互不相等的△ABC中, D,E,F分別是AB,AC,BC邊的中點.連接DE,過點C作CM∥AB交DE的延長線于點M,連接CD、EF交于點N,則圖中全等三角形共有( )
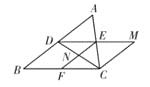
A.3對B.4對C.5對D.6對
【答案】C
【解析】
利用已知條件可證得DE,EF都是△ABC的中位線,同時可證得AE=EC,CF=![]() BC,利用三角形中位線定理可得到DE=
BC,利用三角形中位線定理可得到DE=![]() BC,DE∥BC,EF∥AB,從而可以推出∠EDC=∠FCN,DE=CF,再利用AAS證明△DEN≌△CFN,然后利用有兩組對邊平行的四邊形是平行四邊形,可證得四邊形EFCM是平行四邊形,再利用平行四邊形的性質可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
BC,DE∥BC,EF∥AB,從而可以推出∠EDC=∠FCN,DE=CF,再利用AAS證明△DEN≌△CFN,然后利用有兩組對邊平行的四邊形是平行四邊形,可證得四邊形EFCM是平行四邊形,再利用平行四邊形的性質可以推出△EMC≌△CFE,△ADE≌△CME,△ADE≌△CEF, △BCD≌△MDC.
證明:∵D,E,F分別是AB,AC,BC邊的中點.
∴CF=![]() BC,DE是△ABC的中位線,EF是△ABC的中位線,AE=EC
BC,DE是△ABC的中位線,EF是△ABC的中位線,AE=EC
∴DE=![]() BC,DE∥BC,EF∥AB,
BC,DE∥BC,EF∥AB,
∴∠EDC=∠FCN,DE=CF
在△DEN和△CFN中
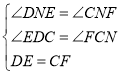
∴△DEN≌△CFN(AAS);
∵EF∥AB,CM∥AB
∴EF∥CM,DE∥BC
∴四邊形EFCM是平行四邊形,
∴EM=CF=DE,EF=CM,
在△EMC和△CFE中,
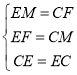
∴△EMC≌△CFE(SSS);
在△ADE和△CME中,

∴△ADE≌△CME(SAS);
∴△ADE≌△CEF,
∴DE∥BC
又BD∥CM∥EF
∴四邊形DBCM是平行四邊形,
∴△BCD≌△MDC
∴圖中的全等三角形一共有5對.
故答案為:C.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,O為AC的中點,直線EF經過點O,并且與AB交于點E,與DC交于點F,∠DFE=∠BFE.
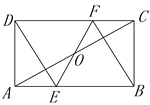
(1)求證:四邊形DEBF是菱形;
(2)若AD=4,AB=8,則線段EF的長是_______.(直接寫出答案即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場以每件10元的價格購進一種商品,試銷中發現,這種商品每天的銷售量m(件)與每件的銷售價x(元)滿足一次函數,其函數圖像如圖所示.

(1)求商場每天銷售這種商品的銷售利潤y(元)與每件的銷售價x(元)之間的函數解析式;
(2)試判斷,每件商品的銷售價格在什么范圍內,每天的銷售利潤隨著價格的提高而增加.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A的坐標是(4,0),并且OA=OC=4OB,動點P在過A,B,C三點的拋物線上.
(1)求拋物線的解析式;
(2)是否存在點P,使得△ACP是以AC為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由;
(3)過動點P作PE垂直于y軸于點E,交直線AC于點D,過點D作x軸的垂線.垂足為F,連接EF,以線段EF的中點G為圓心,以EF為直徑作⊙G,當⊙G最小時,求出點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
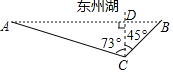
【題目】某市為了創建綠色生態城市,在城東建了“東州湖”景區,小明和小亮想測量“東州湖”東西兩端A、B間的距離.于是,他們去了湖邊,如圖,在湖的南岸的水平地面上,選取了可直接到達點B的一點C,并測得BC=350米,點A位于點C的北偏西73°方向,點B位于點C的北偏東45°方向.請你根據以上提供的信息,計算“東州湖”東西兩端之間AB的長.(結果精確到1米)(參考數據:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
科目:初中數學 來源: 題型:
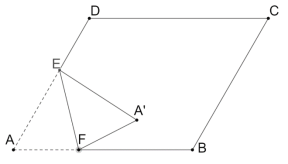
【題目】如圖,在菱形![]() 中,
中,![]() ,
, ![]() , 點
, 點![]() 在邊
在邊![]() 上,且
上,且![]() ,點
,點![]() 為線段
為線段![]() 上一動點(不與點
上一動點(不與點![]() 重合),將菱形沿直線
重合),將菱形沿直線![]() 折疊,點
折疊,點![]() 的對應點為點
的對應點為點![]() ,當
,當![]() 落在菱形的對角線上時,
落在菱形的對角線上時,![]() 的長為__________.
的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把兩條中線互相垂直的三角形稱為“中垂三角形”.例如圖1,圖2,圖3中,![]() ,
,![]() 是
是![]() 的中線,
的中線,![]() ,垂足為
,垂足為![]() .像
.像![]() 這樣的三角形均為“中垂三角形”.設
這樣的三角形均為“中垂三角形”.設![]() ,
,![]() ,
,![]() .
.
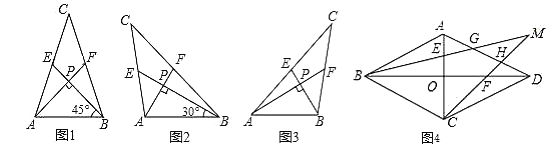
特例探索:
(1)①如圖1,當![]() ,
,![]() 時,
時,![]() _________,
_________,![]() ________;
________;
②如圖2,當![]() ,
,![]() 時,求
時,求![]() 和
和![]() 的值.
的值.
歸納證明:
(2)請你觀察(1)中的計算結果,猜想三者之間的關系,用等式表示出來,并利用圖3證明你發現的關系式.
(3)利用(2)中的結論,解答下列問題:在邊長為3的菱形![]() 中,
中,![]() 為對角線
為對角線![]() ,
,![]() 的交點,
的交點,![]() 分別為線段
分別為線段![]() ,
,![]() 的中點,連接
的中點,連接![]() ,
,![]() 并延長交于點
并延長交于點![]() ,
,![]() ,
,![]() 分別交
分別交![]() 于點
于點![]() ,
,![]() ,如圖4所示,求
,如圖4所示,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,反比例函數y=![]() 的圖象與一次函數y=k(x-2)的圖象交點為A(3,2),B(x,y).
的圖象與一次函數y=k(x-2)的圖象交點為A(3,2),B(x,y).
(1)求反比例函數與一次函數的解析式及B點坐標;
(2)若C是y軸上的點,且滿足△ABC的面積為10,求C點坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com