已知在△ABC中，AB＝8，BC＝15，AC＝17，則下列結(jié)論錯誤的是( )．
A．△ABC是直角三角形，且∠B＝90°
B．
△ABC是直角三角形，且∠A＝60°
C．△ABC是直
角三角形，且AC是它的斜邊
D．△ABC的面積為60
科目：初中數(shù)學(xué) 來源： 題型：
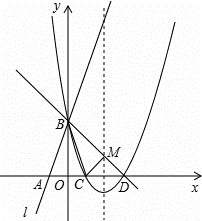
如圖所示，直線l：y=3x+3與x軸交于點A，與y軸交于點B．把△AOB沿y軸翻折，點A落到點C，拋物線過點B、C和D（3，0）．
（1）求直線BD和拋物線的解析式．
（2）若BD與拋物線的對稱軸交于點M，點N在坐標(biāo)軸上，以點N、B、D為頂點的三角形與△MCD相似，求所有滿足條件的點N的坐標(biāo)．
（3）在拋物線上是否存在點P，使S△PBD=6？若存在，求出點P的坐標(biāo)；若不存在，說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
勾股定理是一條古老的數(shù)學(xué)定理，它有很多種證明方法，我國漢代數(shù)學(xué)家趙爽根據(jù)弦圖，利用面積法進(jìn)行證明，著名數(shù)學(xué)家華羅庚曾提出把“數(shù)形關(guān)系”(勾股定理)帶到其他星球，作為地球人與其他星球“人”進(jìn)行第一次“談話”的語言．
[定理表述]
請你根據(jù)圖1中的直角三角形敘述勾股定理(用文字及符號語言敘述)．
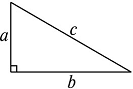
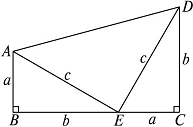
圖1 圖2
[嘗試證明]
以圖1中的直角三角形為基礎(chǔ)，可以構(gòu)造出以a，b為底，以a＋b為高的直角梯形(如圖2)，請你利用圖2，驗證勾股定理．
[知識拓展]
利用圖2中的直角梯形，我們可以證明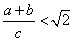
.其證明步驟如下：
∵BC＝a＋b，AD＝__________，
又∵在直角梯形ABCD中有BC__________AD(填大小關(guān)系)，即__________，
∴.
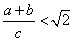查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
某市為嚴(yán)禁酒后駕駛與超速行駛，切實保障交通安全，加強(qiáng)了各項交通督查力度．某次將雷達(dá)測速區(qū)監(jiān)測到的一組汽車的時速數(shù)據(jù)整理，得到其頻數(shù)及頻率如下表(未完成)：
| 數(shù)據(jù)段 | 頻數(shù) | 頻率 |
| 30～40 | 10 | 0.05 |
| 40～50 | 36 | |
| 50～60 |
| 0.39 |
| 60～70 |
| |
| 70～80 | 20 | 0.10 |
| 總計 |
| 1 |
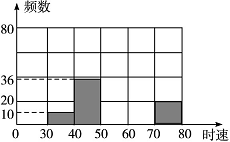
注：30～40為時速大于等于30千米而小于40千米，其他類同．
(1)請你把表中的數(shù)據(jù)填寫完整；
(2)補(bǔ)全頻數(shù)分布直方圖；
(3)如果此地汽車時速不低于60千米即為違章，則違章車輛共有多少輛？
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
AB·BC＝60，無法推出∠A＝60°.
經(jīng)過點A（-2，n），則n的值為（ ）
B、
C、
D、
， MN=2，求圓心O到AB的距離。
，
，－0.5xy＋
，
，
，
中，是分式的有( )．
A．1個 B．2個 C．3個 D．4個