
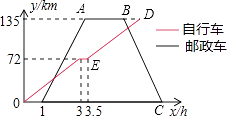
【題目】為倡導低碳生活,綠色出行,某自行車俱樂部利用周末組織“遠游騎行”活動.自行車隊從甲地出發,途徑乙地短暫休息完成補給后,繼續騎行至目的地丙地,自行車隊出發1小時后,恰有一輛郵政車從甲地出發,沿自行車隊行進路線前往丙地,在丙地完成2小時裝卸工作后按原路返回甲地,自行車隊與郵政車行駛速度均保持不變,并且郵政車行駛速度是自行車隊行駛速度的2.5倍,如圖表示自行車隊、郵政車離甲地的路程y(km)與自行車隊離開甲地時間x(h)的函數關系圖象,請根據圖象提供的信息解答下列各題: 
(1)自行車隊行駛的速度是km/h;
(2)郵政車出發多少小時與自行車隊首次相遇?
(3)郵政車在返程途中與自行車隊再次相遇時的地點距離甲地多遠?
【答案】
(1)24
(2)解:由題意得
郵政車的速度為:24×2.5=60km/h.
設郵政車出發a小時兩車相遇,由題意得
24(a+1)=60a,
解得:a= ![]() .
.
答:郵政車出發 ![]() 小時與自行車隊首次相遇
小時與自行車隊首次相遇
(3)解:由題意,得
郵政車到達丙地的時間為:135÷60= ![]() ,
,
∴郵政車從丙地出發的時間為: ![]() ,
,
∴B( ![]() ,135),C(7.5,0).
,135),C(7.5,0).
自行車隊到達丙地的時間為:135÷24+0.5= ![]() +0.5=
+0.5= ![]() ,
,
∴D( ![]() ,135).
,135).
設BC的解析式為y1=k1x+b1,由題意得
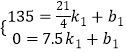 ,
,
∴ ![]() ,
,
∴y1=﹣60x+450,
設ED的解析式為y2=k2x+b2,由題意得
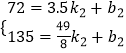 ,
,
解得: ![]() ,
,
∴y2=24x﹣12.
當y1=y2時,
﹣60x+450=24x﹣12,
解得:x=5.5.
y1=﹣60×5.5+450=120.
答:郵政車在返程途中與自行車隊再次相遇時的地點距離甲地120km.
【解析】解:(1)由題意得自行車隊行駛的速度是:72÷3=24km/h.所以答案是:24;(1)由速度=路程÷時間就可以求出結論;(2)由自行車的速度就可以求出郵政車的速度,再由追擊問題設郵政車出發a小時兩車相遇建立方程求出其解即可;(3)由郵政車的速度可以求出B的坐標和C的坐標,由自行車的速度就可以D的坐標,由待定系數法就可以求出BC,ED的解析式就可以求出結論.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】中學生騎電動車上學給交通安全帶來隱患,為了解某中學2 500個學生家長對“中學生騎電動車上學”的態度,從中隨機調查400個家長,結果有360個家長持反對態度,則下列說法正確的是( )
A. 調查方式是普查 B. 該校只有360個家長持反對態度
C. 樣本是360個家長 D. 該校約有90%的家長持反對態度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】講完“有理數的除法”后,老師在課堂上出了一道計算題:15![]() ÷(-8).不一會兒,不少同學算出了答案,老師把班上同學的解題過程歸類寫到黑板上.
÷(-8).不一會兒,不少同學算出了答案,老師把班上同學的解題過程歸類寫到黑板上.
方法一:原式=![]() ×(-
×(-![]() )=-
)=-![]() =-1
=-1![]() ;
;
方法二:原式=(15+![]() )×(-
)×(-![]() )=15×(-
)=15×(-![]() )+
)+![]() ×(-
×(-![]() )=-
)=-![]() =-1
=-1![]() ;
;
方法三:原式=(16-![]() )÷(-8)=16÷(-8)-
)÷(-8)=16÷(-8)-![]() ÷(-8)=-2+
÷(-8)=-2+![]() =-1
=-1![]() .
.
對這三種方法,大家議論紛紛,你認為哪種方法最好?請說出理由,并說說本題對你有何啟發.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年5月,從全國旅游景區質量等級評審會上傳來喜訊,我市“風岡茶海之心”、“赤水佛光巖”、“仁懷中國酒文化城”三個景區加入國家“4A”級景區.至此,全市“4A”級景區已達13個.某旅游公司為了了解我市“4A”級景區的知名度情況,特對部分市民進行現場采訪,根據市民對13個景區名字的回答情況,按答數多少分為熟悉(A),基本了解(B)、略有知曉(C)、知之甚少(D)四類進行統計,繪制了一下兩幅統計圖(不完整),請根據圖中信息解答以下各題: 
(1)本次調查活動的樣本容量是;
(2)調查中屬于“基本了解”的市民有人;
(3)補全條形統計圖;
(4)“略有知曉”類占扇形統計圖的圓心角是多少度?“知之甚少”類市民占被調查人數的百分比是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC的邊長是2,D、E分別為AB、AC的中點,過E點作EF∥DC交BC的延長線于點F,連接CD.
(1)求證:四邊形CDEF是平行四邊形;
(2)求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AD是中線,E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.試判斷四邊形ADCF的形狀,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張矩形紙片ABCD沿直線MN折疊,使點C落在點A處,點D落在點E處,直線MN交BC于點M,交AD于點N. 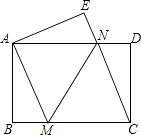
(1)求證:CM=CN;
(2)若△CMN的面積與△CDN的面積比為3:1,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,這是一種數值轉換機的運算程序.
(1)若第1次輸入的數為2,則第1次輸出的數為1,那么第2次輸出的數為4;若第1次輸入的數為12,則第5次輸出的數為__________.
(2)若輸入的數為5,求第2016次輸出的數是多少.
(3)是否存在輸入的數x,使第3次輸出的數是x?若存在,求出所有x的值;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com