
【題目】小明同學對平面圖形進行了自主探究;圖形的頂點數A,被分成的區域數B,線段數C三者之間是否存在確定的數量關系.如圖是他在探究時畫出的5個圖形.
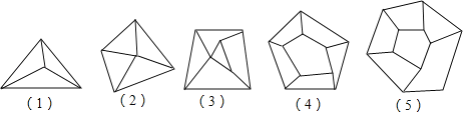
(1)根據圖完成表格:
A | B | C | |
平面圖形(1) |
| 3 | 6 |
平面圖形(2) | 5 |
| 8 |
平面圖形(4) | 10 | 6 |
|
(2)猜想:一個平面圖形中頂點數A,區域數B,線段數C之間的數量關系是 ;
(3)計算:已知一個平面圖形有24條線段,被分成9個區域,則這個平面圖形的頂點有 個.
【答案】(1)4、4、15;(2)A+B﹣C=1;(3)16.
【解析】
(1)觀察圖形可填表即可;
(2)先根據題(1)得到的表格數據,可得出平面圖形(1)、(2)、(4)中滿足的關系式,再歸納類推出一般規律;
(3)根據(2)中所得關系即可求解
(1)觀察圖形可知:
平面圖形(1)中頂點數A為4
平面圖形(2)中區域數B為4
平面圖形(3)中線段數C為15
故答案為4、4、15;
(2)由題(1)得到的結果,觀察表格數據可知:
平面圖形(1)中頂點數、區域數、線段數滿足:![]()
平面圖形(2)中頂點數、區域數、線段數滿足:![]()
平面圖形(3)中頂點數、區域數、線段數滿足:![]()
猜想:一個平面圖形中頂點數A,區域數B,線段數C之間的數量關系為![]()
故答案為:![]() ;
;
(3)已知一個平面圖形有24條線段,被分成9個區域,
即![]() ,代入
,代入![]() 中
中
解得:![]()
則這個平面圖形的頂點有16個
故答案為16.


 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】近幾年后,實驗中學準備搬遷新校舍,在遷入新校舍之前,同學們就學校學生如何到校問題進行了一次調查,并將調查結果制成了表格、條形圖和扇形統計圖,請你根據圖表信息完成下列各題:
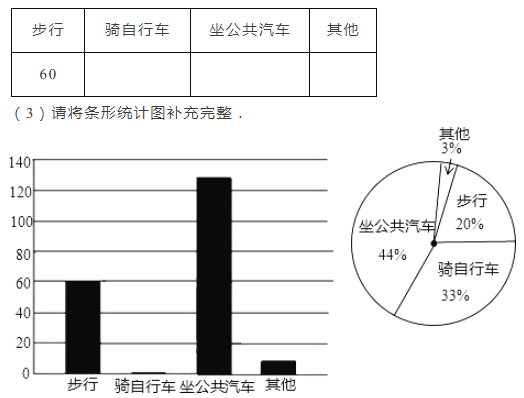
1.(1)此次共調查了多少位學生?
2.(2)請將表格填充完整;
3.(3)請將條形統計圖補充完整.
查看答案和解析>>
科目:初中數學 來源: 題型:
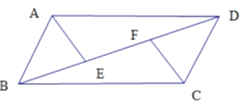
【題目】如圖,在口ABCD中,點E、F是對角線BD上的兩點,且BF=DE,連接AE、CF.
.求證:AE//CF.
【答案】證明見解析
【解析】試題分析:根據平行四邊形的性質可得AD=CB,∠ADE=∠CBF,利用SAS判定△ADE≌△CBF,根據全等三角形的性質即可得∠AED=∠BFC,所以AE∥CF.
試題解析:
∵四邊形ABCD是平行四邊形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
又∵DE=BF,
∴△ADE≌△CBF,
∴∠AED=∠BFC,
∴AE∥CF.
【題型】解答題
【結束】
22
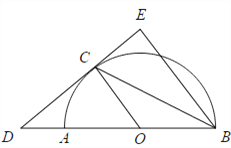
【題目】如圖,已知![]() 是
是![]() 的直徑,CD與
的直徑,CD與![]() 相切于C,
相切于C, ![]() .
.
(1)求證:BC 是![]() 的平分線.
的平分線.
(2)若DC=8, ![]() 的半徑OA=6,求CE的長.
的半徑OA=6,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司為了了解員工每人所創年利潤情況,公司從各部抽取部分員工對每年所創年利潤情況進行統計,并繪制如圖1,圖2統計圖.
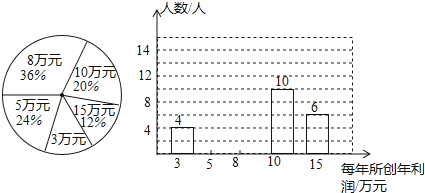
(1)求抽取員工總人數,并將圖補充完整;
(2)每人所創年利潤的眾數是 ,每人所創年利潤的中位數是 ,平均數是 ;
(3)若每人創造年利潤10萬元及(含10萬元)以上為優秀員工,在公司1200員工中有多少可以評為優秀員工?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在同一平面內,∠AOB=150°,∠COD=90°,OE平分∠BOD.
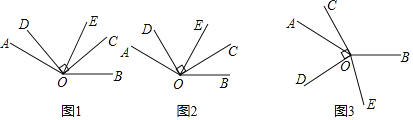
(1)當∠COD的位置如圖1所示時,若∠COE=25°,則∠AOD= ;
(2)當∠COD的位置如圖2所示時,若∠AOE=90°,則∠AOD= ;
(3)當∠COD的位置如圖3所示時,若∠BOE=![]() ∠AOC,求∠AOD的度數.
∠AOC,求∠AOD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】工業園區某機械廠的一個車間主要負責生產螺絲和螺母,該車間有工人44人,其中女生人數比男生人數的![]() 倍少
倍少![]() 人,每個工人平均每天可以生產螺絲
人,每個工人平均每天可以生產螺絲![]() 個或者螺母
個或者螺母![]() 個
個
(1)該車間有男生、女生各多少人?
(2)已知一個螺絲與兩個螺母配套,為了使每天生產的螺絲螺母恰好配套,應該分配多少工人負責生產螺絲,多少工人負責生產螺母?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下面給出的數軸,解答下面的問題:

(1)請你根據圖中A,B兩點的位置,分別寫出它們所表示的有理數A: B: ;
(2)觀察數軸,與點A的距離為![]() 的點表示的數是: ;
的點表示的數是: ;
(3)若將數軸折疊,使得![]() 點與0表示的點重合,則B點與數 表示的點重合;
點與0表示的點重合,則B點與數 表示的點重合;
(4)若數軸上M、N兩點之間的距離為2019(M在N的左側),且M、N兩點經過(3)中折疊后互相重合,則![]() 、
、![]() 兩點表示的數分別是:M: ,N: .
兩點表示的數分別是:M: ,N: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,正方形紙片ABCD的邊長為2,翻折∠B、∠D,使兩個直角的頂點重合于對角線BD上一點P、EF、GH分別是折痕(如圖2).設AE=x(0<x<2),給出下列判斷:①當x=1時,點P是正方形ABCD的中心;②當x=![]() 時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
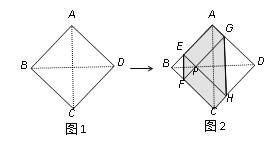
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
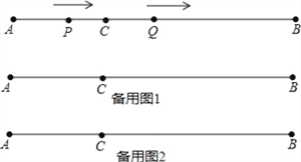
【題目】如圖,AB=12cm,點C是線段AB上的一點,BC=2AC.動點P從點A出發,以3cm/s的速度向右運動,到達點B后立即返回,以3cm/s的速度向左運動;動點Q從點C出發,以1cm/s的速度向右運動.設它們同時出發,運動時間為ts.當點P與點Q第二次重合時,P、Q兩點停止運動.
(1)AC=__cm,BC=__cm;
(2)當t為何值時,AP=PQ;
(3)當t為何值時,PQ=1cm.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com