某停車場的收費
標準如下：中型汽車的停車費為
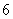元/輛，小型汽車的停車費為
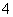元/輛.現在停車場共有
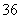輛中、小型汽車，這些車共繳納停車費
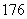元.問中、小
型汽車各有多少輛？
名題金卷系列答案科目：初中數學 來源： 題型：
反比例函數y＝
(k為常數,k≠0)的圖象是雙曲線.當k＞0時，雙曲線兩個分支分別在
一、三象限,在每一個象限內,y隨x的增大而減小（簡稱增減性）；反比例函數的圖象關于
原點對稱（簡稱對稱性）．
這些我們熟悉的性質，可以通過說理得到嗎？
【嘗試說理】
我們首先對反比例函數y＝（k＞0）的增減性來進行說理．
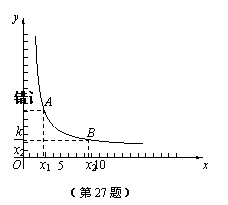
如圖，當x＞0時．
在函數圖象上任意取兩點A、B，設A(x1，
)，B(x2，
)，
且0＜x1＜ x2．
下面只需要比較和的大小．
—＝
．
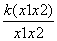∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
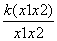∴＜0．即＜ ．
這說明：x1＜ x2時，＞．也就是：自變量值增大了，對應的函數值反而變小了．
即：當x＞0時，y隨x的增大而減小．
同理，當x＜0時，y隨x的增大而減小．
（1）試說明：反比例函數y＝ （k＞0）的圖象關于原點對稱．
【運用推廣】
（2）分別寫出二次函數y＝ax2 (a＞0，a為常數)的對稱性和增減性，并進行說理．
對稱性： ；
增減性： ．
說理：
（3）對于二次函數y＝ax2＋bx＋c (a＞0，a，b，c為常數)，請你從增減性的角度，簡要解釋為何當x＝—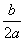
時函數取得最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
某市抽樣調查了全市40個噪聲測量點在某時刻的噪聲聲級（單位：dB），將調查的數
據進行處理（設所測數據是正整數），得頻數分布表如下：
| 組 別 | 噪聲聲級分組 | 頻 數 | 頻 率 |
| 1 | 44.5——59.5 | 4 | 0.1 |
| 2 | 59.5——74.5 | 8 | 0.2 |
| 3 | 74.5——89.5 | 10 | 0.25 |
| 4 | 89.5——104.5 | b | c |
| 5 | 104.5——119.5 | 6 | 0.15 |
| 合 計 | 40 | 1.00 |
則第四小組的頻率c =_________．
查看答案和解析>>
科目：初中數學 來源： 題型：
已知：如圖，在菱形ABCD中，∠B= 60°，把一個含60°角的三角尺與這個
菱形疊合，使三角尺60°角的頂點與點A重合，將三角尺繞點A按逆時針方向旋轉 ．
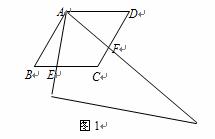
(1)如圖1，當三角尺的兩邊分別與菱形的兩邊BC、CD相交于點E、F．
求證：CE+CF=AB；
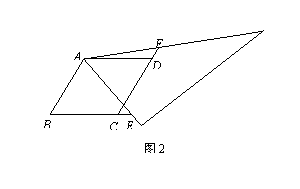
(2)如圖2，當三角尺的兩邊分別與菱形的兩邊BC、CD的延長線相交于點E、F．寫出此時CE、CF、AB長度之間關系的結論．（不需要證明）
|
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
輛，小型汽車有
輛， 
0輛. 
，則
的值為__________．
.
B．
D．
，
要使
≌
，若以“SAS”為依據，補充的條件是 . 