
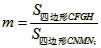 ,請問m是否為定值?若是,請求出m的值;若不是,請說明理由;
,請問m是否為定值?若是,請求出m的值;若不是,請說明理由;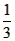 ,Q為AE上一點且QF=
,Q為AE上一點且QF=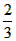 ,拋物線y=mx2+bx+c經過C、Q兩點,請求出此拋物線的解析式;
,拋物線y=mx2+bx+c經過C、Q兩點,請求出此拋物線的解析式;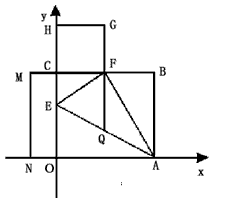
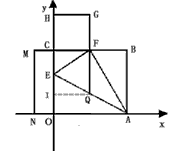
| 解:(1)EO>EC, 理由如下:由折疊知,EO=EF, 在Rt△EFC中,EF為斜邊, ∴EF>EC, 故EO>EC; (2)m為定值, ∵S四邊形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO―EC)=CO·(EO-EC) S四邊形CMNO=CM·CO=|CE-EO|·CO=(EO-EC)·CO ∴ 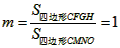 ; ;(3)∵CO=1, 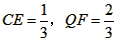 ∴EF=EO= 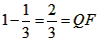 ∴cos∠FEC= 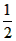 ∴∠FEC=60°, ∴ 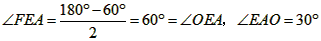 ∴△EFQ為等邊三角形, 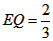 作QI⊥EO于I,EI= 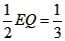 ,IQ= ,IQ=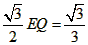 ∴IO= 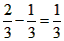 ∴Q點坐標為 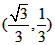 ∵拋物線y=mx2+bx+c過點C(0,1),Q 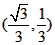 ,m=1 ,m=1 ∴可求得 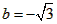 ,c=1 ,c=1 ∴拋物線解析式為 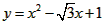 ; ;(4)由(3), 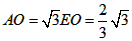 當 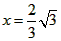 時, 時,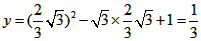 <AB <AB ∴P點坐標為 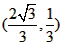 , ,∴BP= 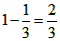 AO AO 若△PBK與△AEF相似,而△AEF≌△AEO,則分情況如下: ①  時, 時,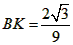 ∴K點坐標為  或 或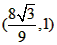 ② 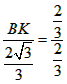 時, 時,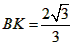 ∴K點坐標為 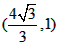 或 或 故直線KP與y軸交點T的坐標為 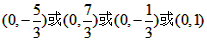 。 。 |
 |


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |

查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |

查看答案和解析>>
科目:初中數學 來源: 題型:
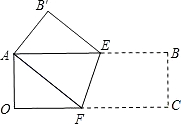
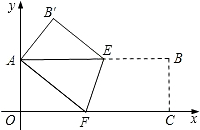
 已知,如圖所示,矩形OABC在平面直角坐標系中,矩形各頂點分別為O(0,0),A(0,6),B(8,6),C(8,0).點D(0,3)在OA上,點E(4,0)在OC上,連接DE,將△DOE繞O點逆時針旋轉,旋轉角為α(0°<α<360°),得到△D′OE′,連接AD′,當∠AD′O=90°時,
已知,如圖所示,矩形OABC在平面直角坐標系中,矩形各頂點分別為O(0,0),A(0,6),B(8,6),C(8,0).點D(0,3)在OA上,點E(4,0)在OC上,連接DE,將△DOE繞O點逆時針旋轉,旋轉角為α(0°<α<360°),得到△D′OE′,連接AD′,當∠AD′O=90°時,查看答案和解析>>
科目:初中數學 來源:同步題 題型:解答題
 在直角坐標系中,OA=6,OC=8,若將矩形折疊,使點B與O重合,得到折痕EF。
在直角坐標系中,OA=6,OC=8,若將矩形折疊,使點B與O重合,得到折痕EF。 

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com