
【題目】△ABC中,∠C=90°,點O為△ABC三條角平分線的交點,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,則點O到三邊AB、AC、BC的距離為( )
A.2cm,2cm,2cmB.3cm,3cm,3cmC.4cm,4cm,4cmD.2cm,3cm,5cm
【答案】A
【解析】
連接OA,OB,OC,利用角的平分線上的點到角的兩邊的距離相等可知△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,所以BD=BF,CD=CE,AE=AF,又因為點O到三邊AB、AC、BC的距離是CD,所以AB=8-CD+6-CD=10,解得CD=2,所以點O到三邊AB、AC、BC的距離為2.
連接OA,OB,OC,則△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,
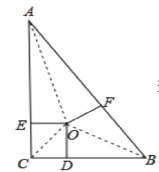
∴BD=BF,CD=CE,AE=AF,
又∵∠C=90°,OD⊥BC于D,OE⊥AC于E,且O為△ABC三條角平分線的交點
∴四邊形OECD是正方形,
則點O到三邊AB、AC、BC的距離=CD,
∴AB=8CD+6CD=2CD+14,又根據(jù)勾股定理可得:AB=10,
即2CD+14=10
∴CD=2,
即點O到三邊AB、AC、BC的距離為2cm.
故選A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,O是直線![]() 上一點,
上一點,![]() 是一條射線,
是一條射線,![]() 平分
平分![]() ,
,![]() 在
在![]() 內,
內,![]() .
.
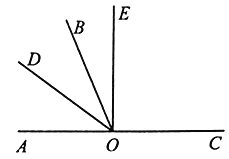
(1)若![]() ,垂足為O點,則
,垂足為O點,則![]() 的度數(shù)為________°,
的度數(shù)為________°,![]() 的度數(shù)為________°;在圖中,與
的度數(shù)為________°;在圖中,與![]() 相等的角有_________;
相等的角有_________;
(2)若![]() ,求
,求![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,A、B、C是正方形網(wǎng)格中的三個格點.
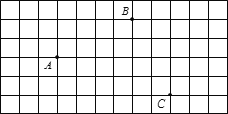
(1)①畫射線AC;
②畫線段BC;
③過點B畫AC的平行線BD;
④在射線AC上取一點E,畫線段BE,使其長度表示點B到AC的距離;
(2)在(1)所畫圖中,
①BD與BE的位置關系為 ;
②線段BE與BC的大小關系為BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】【問題引入】
已知:如圖BE、CF是ΔABC的中線,BE、CF相交于G。求證: ![]()
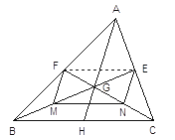
證明:連結EF
∵E、F分別是AC、AB的中點
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)連結AG并延長AG交BC于H,點H是否為BC中點 (填“是”或“不是”)
(2)①如果M、N分別是GB、GC的中點,則四邊形EFMN 是 四邊形。
②當![]() 的值為 時,四邊形EFMN 是矩形。
的值為 時,四邊形EFMN 是矩形。
③當![]() 的值為 時,四邊形EFMN 是菱形。
的值為 時,四邊形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,則四邊形EFMN的面積![]() =_________
=_________
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下列材料:
由于發(fā)展時間早、發(fā)展速度快,經(jīng)過20多年大規(guī)模的高速開發(fā)建設,北京四環(huán)內,甚至五環(huán)內可供開發(fā)建設的土地資源越來越稀缺,更多的土地供應將集中在五環(huán)外,甚至六環(huán)外的遠郊區(qū)縣.
據(jù)中國經(jīng)濟網(wǎng)2017年2月報道,來自某市場研究院的最新統(tǒng)計,2016年,剔除了保障房后,在北京新建商品住宅交易量整體上漲之時,北京各區(qū)域的新建商品住宅交易量則是有漲有跌![]() 其中,昌平、通州、海淀、朝陽、西城、東城六區(qū)下跌,跌幅最大的為朝陽區(qū),新建商品住宅成交量比2015年下降了
其中,昌平、通州、海淀、朝陽、西城、東城六區(qū)下跌,跌幅最大的為朝陽區(qū),新建商品住宅成交量比2015年下降了![]() 而延慶、密云、懷柔、平谷、門頭溝、房山、順義、大興、石景山、豐臺十區(qū)的新建商品住宅成交量表現(xiàn)為上漲,漲幅最大的為順義區(qū),比2015年上漲了
而延慶、密云、懷柔、平谷、門頭溝、房山、順義、大興、石景山、豐臺十區(qū)的新建商品住宅成交量表現(xiàn)為上漲,漲幅最大的為順義區(qū),比2015年上漲了![]() 另外,從環(huán)線成交量的占比數(shù)據(jù)上,同樣可以看出成交日趨郊區(qū)化的趨勢
另外,從環(huán)線成交量的占比數(shù)據(jù)上,同樣可以看出成交日趨郊區(qū)化的趨勢![]() 根據(jù)統(tǒng)計,2008年到2016年,北京全市成交的新建商品住宅中,二環(huán)以內的占比逐步從
根據(jù)統(tǒng)計,2008年到2016年,北京全市成交的新建商品住宅中,二環(huán)以內的占比逐步從![]() 下降到了
下降到了![]() ;二、三環(huán)之間的占比從
;二、三環(huán)之間的占比從![]() 下降到了
下降到了![]() ;三、四環(huán)之間的占比從
;三、四環(huán)之間的占比從![]() 下降到了
下降到了![]() ;四、五環(huán)之間的占比從
;四、五環(huán)之間的占比從![]() 下降到了
下降到了![]() 也就是說,整體成交中位于五環(huán)之內的新房占比,從2008年的
也就是說,整體成交中位于五環(huán)之內的新房占比,從2008年的![]() 下降到了2016年的
下降到了2016年的![]() ,下滑趨勢非常明顯
,下滑趨勢非常明顯![]() 由此可見,新房市場的遠郊化是北京房地產市場發(fā)展的大勢所趨
由此可見,新房市場的遠郊化是北京房地產市場發(fā)展的大勢所趨![]() 注:占比,指在總數(shù)中所占的比重,常用百分比表示
注:占比,指在總數(shù)中所占的比重,常用百分比表示![]()
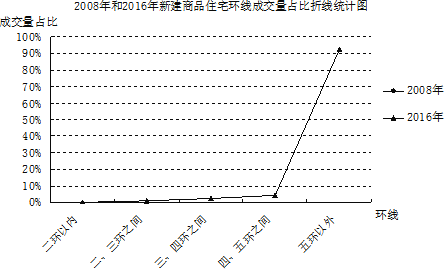
根據(jù)以上材料解答下列問題:
![]() 補全折線統(tǒng)計圖;
補全折線統(tǒng)計圖;
![]() 根據(jù)材料提供的信息,預估2017年位于北京市五環(huán)之內新建商品住宅成交量占比約______ ,你的預估理由是______ .
根據(jù)材料提供的信息,預估2017年位于北京市五環(huán)之內新建商品住宅成交量占比約______ ,你的預估理由是______ .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,![]() 的頂點坐標分別是
的頂點坐標分別是![]() ,對于
,對于![]() 的橫長、縱長、縱橫比給出如下定義:
的橫長、縱長、縱橫比給出如下定義:
將![]() 中的最大值,稱為
中的最大值,稱為![]() 的橫長,記作
的橫長,記作![]() ;將
;將![]() 中的最大值,稱為
中的最大值,稱為![]() 的縱長,記作
的縱長,記作![]() ;將
;將![]() 叫做
叫做![]() 的縱橫比,記作
的縱橫比,記作![]() .
.
例如:如圖![]() 的三個頂點的坐標分別是
的三個頂點的坐標分別是![]() ,則
,則![]() ,
,
所以![]() .
.
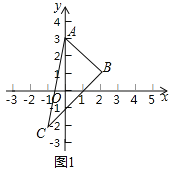
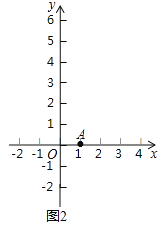
![]() 如圖2,點
如圖2,點![]() ,
,
![]() 點
點![]() ,
,
則![]() 的縱橫比
的縱橫比![]() ______
______
![]() 的縱橫比
的縱橫比![]() ______;
______;
![]() 點F在第四象限,若
點F在第四象限,若![]() 的縱橫比為1,寫出一個符合條件的點F的坐標;
的縱橫比為1,寫出一個符合條件的點F的坐標;
![]() 點M是雙曲線
點M是雙曲線![]() 上一個動點,若
上一個動點,若![]() 的縱橫比為1,求點M的坐標;
的縱橫比為1,求點M的坐標;
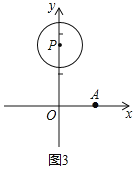
![]() 如圖3,點
如圖3,點![]() 以
以![]() 為圓心,1為半徑,點N是
為圓心,1為半徑,點N是![]() 上一個動點,直接寫出
上一個動點,直接寫出![]() 的縱橫比
的縱橫比![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列說法中正確的是( )
A.有且只有一條直線與已知直線垂直;
B.從直線外一點到這條直線的垂線段,叫做這點到這條直線距離;
C.互相垂直的兩條線段一定相交;
D.直線![]() 外一點
外一點![]() 與直線
與直線![]() 上各點連接而成的所有線段中,最短線段的長度是
上各點連接而成的所有線段中,最短線段的長度是![]() ,則點
,則點![]() 到直線
到直線![]() 的距離是
的距離是![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】以直線AB上一點O為端點作射線 OC,使∠BOC=60°,將一個直角三角形的直角頂點放在點O處.(注:∠DOE=90°)
(1)如圖1,若直角三角板DOE的一邊OD放在射線OB上,則∠COE= °;
(2)如圖2,將直角三角板DOE繞點O逆時針方向轉動到某個位置,若OE恰好平分∠AOC,請說明OD所在射線是∠BOC的平分線;
(3)如圖3,將三角板DOE繞點O逆時針轉動到某個位置時,若恰好∠COD= ![]() ∠AOE,求∠BOD的度數(shù)?
∠AOE,求∠BOD的度數(shù)?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
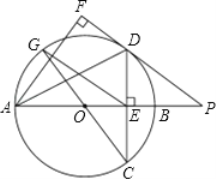
【題目】如圖,在⊙O中,直徑AB垂直弦CD于E,過點A作∠DAF=∠DAB,過點D作AF的垂線,垂足為F,交AB的延長線于點P,連接CO并延長交⊙O于點G,連接EG.
(1)求證:DF是⊙O的切線;
(2)若AD=DP,OB=3,求![]() 的長度;
的長度;
(3)若DE=4,AE=8,求線段EG的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com