
定義1:在△ABC中,若頂點A,B,C按逆時針方向排列,則規(guī)定它的面積為“有向面積”;若頂點A,B,C按順時針方向排列,則規(guī)定它的面積的相反數(shù)為△ABC的“有向面積”.“有向面積”用 表示,例如圖1中,
表示,例如圖1中, ,圖2中,
,圖2中, .
.
定義2:在平面內(nèi)任取一個△ABC和點P(點P不在△ABC的三邊所在直線上),稱有序數(shù)組( ,
, ,
, )為點P關(guān)于△ABC的“面積坐標(biāo)”,記作
)為點P關(guān)于△ABC的“面積坐標(biāo)”,記作 ,例如圖3中,菱形ABCD的邊長為2,
,例如圖3中,菱形ABCD的邊長為2, ,則
,則 ,點G關(guān)于△ABC的“面積坐標(biāo)”
,點G關(guān)于△ABC的“面積坐標(biāo)” 為
為 .在圖3中,我們知道
.在圖3中,我們知道 ,利用“有向面積”,我們也可以把上式表示為:
,利用“有向面積”,我們也可以把上式表示為: .
.
應(yīng)用新知:
(1)如圖4,正方形ABCD的邊長為1,則 ,點D關(guān)于△ABC的“面積坐標(biāo)”是 ;探究發(fā)現(xiàn):
,點D關(guān)于△ABC的“面積坐標(biāo)”是 ;探究發(fā)現(xiàn):
(2)在平面直角坐標(biāo)系 中,點
中,點 ,
,
①若點P是第二象限內(nèi)任意一點(不在直線AB上),設(shè)點P關(guān)于 的“面積坐標(biāo)”為
的“面積坐標(biāo)”為 ,
,
試探究 與
與 之間有怎樣的數(shù)量關(guān)系,并說明理由;
之間有怎樣的數(shù)量關(guān)系,并說明理由;
②若點 是第四象限內(nèi)任意一點,請直接寫出點P關(guān)于
是第四象限內(nèi)任意一點,請直接寫出點P關(guān)于 的“面積坐標(biāo)”(用x,y表示);
的“面積坐標(biāo)”(用x,y表示);
解決問題:
(3)在(2)的條件下,點 ,點Q在拋物線
,點Q在拋物線 上,求當(dāng)
上,求當(dāng) 的值最小時,點Q的橫坐標(biāo).
的值最小時,點Q的橫坐標(biāo).
(1)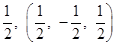 ;(2)①
;(2)①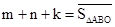 ;②
;②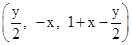 ;(3)
;(3)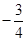 .
.
解析試題分析:(1)直接根據(jù)“有向面積”和“ 面積坐標(biāo)”的定義寫出即可.
(2)①分點P在△ABO外部和當(dāng)點P在△ABO內(nèi)部兩種情況討論即可.
②直接根據(jù) “ 面積坐標(biāo)”的定義寫出即可.
(3)分點Q在第二象限,點Q在第一象限和點Q在y軸上三種情況討論即可.
試題解析:(1)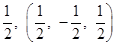 .
.
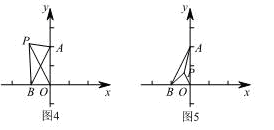
(2)①當(dāng)點P在△ABO外部時,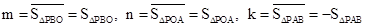 ,
,
∴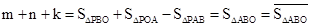 .
.
當(dāng)點P在△ABO內(nèi)部時,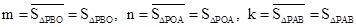 ,
,
∴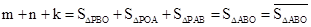 .
.
綜上所述,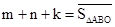 .
.
②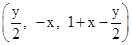 .
.
(3)∵點Q在拋物線 上,∴設(shè)
上,∴設(shè)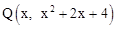 .
.
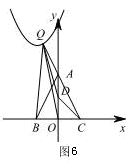
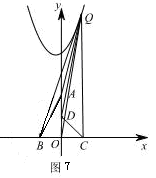
①當(dāng)點Q在第二象限時, ,由圖6可知,
,由圖6可知,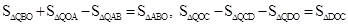 ,
,
由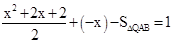 得
得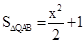 ;
;
由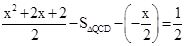 得
得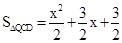 .
.
∴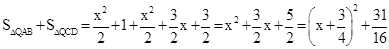 .
.
∴當(dāng)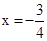 時,
時,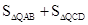 的最小值為
的最小值為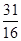 .
.
②當(dāng)點Q在第一象限時,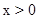 ,由圖7可知,
,由圖7可知,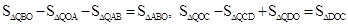 ,
,
由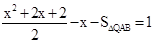 得
得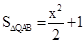 ;
;
由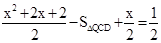 得
得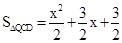 .
.
∴ .
.
∴此時,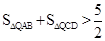 無最小值.
無最小值.
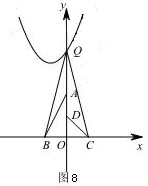
③當(dāng)點Q為 與y軸的交點時,Q(0,4),
與y軸的交點時,Q(0,4),
由圖8可知,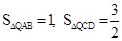 ,∴
,∴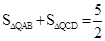 .
.
綜上所述,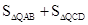 的最小值為
的最小值為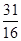 ,此時,點Q的橫坐標(biāo)為
,此時,點Q的橫坐標(biāo)為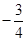 .
.
考點:1.新定義和閱讀型;2.點的坐標(biāo);3.二次函數(shù)的性質(zhì);4.分類思想的應(yīng)用.


科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,已知拋物線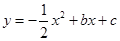 圖象經(jīng)過A(-1,0),B(4,0)兩點.
圖象經(jīng)過A(-1,0),B(4,0)兩點.
(1)求拋物線的解析式;
(2)若C(m,m-1)是拋物線上位于第一象限內(nèi)的點,D是線段AB上的一個動點(不與A、B重合),過點D分別作DE∥BC交AC于E,DF∥AC交BC于F.
①求證:四邊形DECF是矩形;
②連結(jié)EF,線段EF的長是否存在最小值?若存在,求出EF的最小值;若不存在,請說明理由.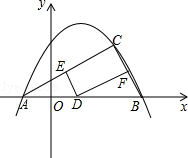
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖①,已知等腰梯形ABCD的周長為48,面積為S,AB∥CD,∠ADC=60°,設(shè)AB=3x.
(1)用x表示AD和CD;
(2)用x表示S,并求S的最大值;
(3)如圖②,當(dāng)S取最大值時,等腰梯形ABCD的四個頂點都在⊙O上,點E和點F分別是AB和CD的中點,求⊙O的半徑R的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
在平面直角坐標(biāo)系 中,拋物線
中,拋物線 經(jīng)過點
經(jīng)過點 (0,
(0, ),
), (3,4).
(3,4).
(1)求拋物線的表達(dá)式及對稱軸;
(2)設(shè)點 關(guān)于原點的對稱點為
關(guān)于原點的對稱點為 ,點
,點 是拋物線對稱軸上一動點,記拋物線在
是拋物線對稱軸上一動點,記拋物線在 ,
, 之間的部分為圖象
之間的部分為圖象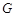 (包含
(包含 ,
, 兩點).若直線
兩點).若直線 與圖象
與圖象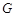 有公共點,結(jié)合函數(shù)圖像,求點
有公共點,結(jié)合函數(shù)圖像,求點 縱坐標(biāo)
縱坐標(biāo)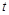 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,直線 與x軸,y軸分別相交于點B,點C,經(jīng)過B、C兩點的拋物線
與x軸,y軸分別相交于點B,點C,經(jīng)過B、C兩點的拋物線 與x軸的另一交點為A,頂點為P,且對稱軸是直線
與x軸的另一交點為A,頂點為P,且對稱軸是直線 .
.
(1)求A點的坐標(biāo)及該拋物線的函數(shù)表達(dá)式;
(2)求出∆PBC的面積;
(3)請問在對稱軸 右側(cè)的拋物線上是否存在點Q,使得以點A、B、C、Q所圍成的四邊形面積是∆PBC的面積的
右側(cè)的拋物線上是否存在點Q,使得以點A、B、C、Q所圍成的四邊形面積是∆PBC的面積的 ?若存在,請求出點Q的坐標(biāo);若不存在,請說明理由.
?若存在,請求出點Q的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,二次函數(shù) 的圖象交x軸于A(﹣1,0),B(2,0),交y軸于C(0,﹣2),過A,C畫直線.
的圖象交x軸于A(﹣1,0),B(2,0),交y軸于C(0,﹣2),過A,C畫直線.
(1)求二次函數(shù)的解析式;
(2)點P在x軸正半軸上,且PA=PC,求OP的長;
(3)點M在二次函數(shù)圖象上,以M為圓心的圓與直線AC相切,切點為H.
①若M在y軸右側(cè),且△CHM∽△AOC(點C與點A對應(yīng)),求點M的坐標(biāo);
②若⊙M的半徑為  ,求點M的坐標(biāo).
,求點M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系中,直線 與拋物線
與拋物線 交于A、B兩點,點A在x軸上,點B的橫坐標(biāo)為-8.
交于A、B兩點,點A在x軸上,點B的橫坐標(biāo)為-8.
(1)求該拋物線的解析式;
(2)點P是直線AB上方的拋物線上一動點(不與點A、B重合),過點P作x軸的垂線,垂足為C,交直線AB于點D,作PE⊥AB于點E.
①設(shè)△PDE的周長為l,點P的橫坐標(biāo)為x,求l關(guān)于x的函數(shù)關(guān)系式,并求出l的最大值;
②連接PA,以PA為邊作圖示一側(cè)的正方形APFG.隨著點P的運動,正方形的大小、位置也隨之改變.當(dāng)頂點F或G恰好落在y軸上時,直接寫出對應(yīng)的點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖所示,已知二次函數(shù) 經(jīng)過
經(jīng)過 、
、 、C三點,點
、C三點,點 是拋物線與直線
是拋物線與直線 的一個交點.
的一個交點.
(1)求二次函數(shù)關(guān)系式和點C的坐標(biāo);
(2)對于動點 ,求
,求 的最大值;
的最大值;
(3)若動點M在直線 上方的拋物線運動,過點M做x軸的垂線交x軸于點F,如果直線AP把線段MF分成1:2的兩部分,求點M的坐標(biāo)。
上方的拋物線運動,過點M做x軸的垂線交x軸于點F,如果直線AP把線段MF分成1:2的兩部分,求點M的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,拋物線 交坐標(biāo)軸于A、B、D三點,過點D作
交坐標(biāo)軸于A、B、D三點,過點D作 軸的平行線交拋物線于點C.直線l過點E(0,-
軸的平行線交拋物線于點C.直線l過點E(0,-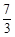 ),且平分梯形ABCD面積.
),且平分梯形ABCD面積.
⑴ 直接寫出A、B、D三點的坐標(biāo);
⑵ 直接寫出直線l的解析式;
⑶ 若點P在直線l上,且在x軸上方,tan∠OPB=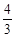 ,求點P的坐標(biāo).
,求點P的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com