
已知AB∥CD,分別探討下列四個圖形中∠APC和∠A、∠C的關系,并選擇圖(1)、(2)之一說明理由。 (10分)

(1) (2) (3) (4)
說理見解析.
【解析】
試題分析:①首先過點P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根據兩直線平行,同旁內角互補,即可求得∠PBA+∠1=180°,∠2+∠PCD=180°,則可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;
②首先過點P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根據兩直線平行,內錯角相等,即可得∠1=∠PAB,∠2=∠PCD,則可得∠APC=∠PAB+∠PCD;
③由AB∥CD,根據兩直線平行,同位角相等,即可得∠1=∠PCD,然后由三角形外角的性質,即可求得∠PCD=∠PAB+∠APC;
④由AB∥CD,根據兩直線平行,內錯角相等,即可得∠1=∠PAB,然后由三角形外角的性質,即可求得∠PAB=∠PCD+∠APC.
試題解析:如圖:
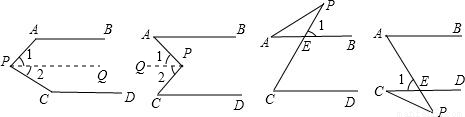
①過點P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
②過點P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD;
③∵AB∥CD,
∴∠1=∠PCD,
∵∠1=∠PAB+∠APC,
∴∠PCD=∠PAB+∠APC;
④∵AB∥CD,
∴∠1=∠PAB,
∵∠1=∠PCD+∠APC,
∴∠PAB=∠PCD+∠APC.
考點:平行線的性質.


科目:初中數學 來源:名師精選(解析版)2 題型:選擇題
三角形的兩邊長分別為3和6,第三邊的長是方程x2-6x+8=0的一個根,則這個三角形的周長是( )
A.9 B.11 C.13 D.14
查看答案和解析>>
科目:初中數學 來源:2016屆遼寧省丹東市七年級下學期期中考試數學試卷(解析版) 題型:解答題
利用乘法公式簡算:
(1) 1102-109×111 (2)98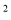 (3)(x+3y+2)(x—3y+2)
(3)(x+3y+2)(x—3y+2)
查看答案和解析>>
科目:初中數學 來源:2016屆貴州省七年級下學期期末考試數學試卷(解析版) 題型:填空題
把m個練習本分給n個學生,如果每人分3本,那么余80本;如果每人分5本,那么最后一個同學有練習本但不足5本,n的值為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com