【題目】如圖，在平面直角坐標系中，點A在第一象限，⊙A與x軸交于B（2，0）、C（8，0）兩點，與y軸相切于點D，則點A的坐標是（ ）
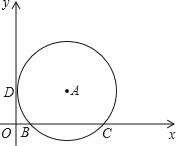
A. （5，4） B. （4，5） C. （5，3） D. （3，5）
【答案】A
【解析】
因為點A在第一象限，⊙A與x軸交于B（2，0）、C（8，0）兩點，與y軸相切于點D，所以OB=2，OC=8，BC=6，連接AD，則AD⊥OD，過點A作AE⊥OC于E，則ODAE是矩形，由垂徑定理可知BE=EC=3，所以OE=AD=5，再連接AB，則AB=AD=5，利用勾股定理可求出AE=4，從而就求出了A的坐標．
連接AD，AB，AC，再過點A作AE⊥OC于E，
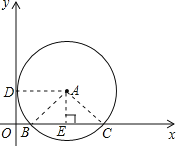
則ODAE是矩形，
∵點A在第一象限，⊙A與x軸交于B（2，0）、C（8，0）兩點，與y軸相切于點D，
∴OB=2，OC=8，BC=6，
∵⊙A與y軸相切于點D，
∴AD⊥OD，
∵由垂徑定理可知：BE=EC=3，
∴OE=AD=5，
∴AB=AD=5，
利用勾股定理知AE=4，
∴A（5，4）．
故選：A．
激活思維優加課堂系列答案
活力試卷系列答案
課課優能力培優100分系列答案科目：初中數學 來源： 題型：
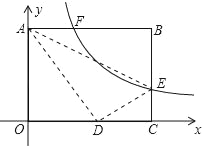
【題目】如圖，矩形ABCO的頂點B（10，8），點A，C在坐標軸上，E是BC邊上一點，將△ABE沿AE折疊，點B剛好與OC邊上點D重合，過點E的反比例函數y＝
的圖象與邊AB交于點F，則線段BF的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
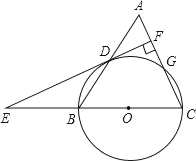
【題目】如圖，在等腰△ABC中，AC＝BC＝10，以BC為直徑作⊙O交AB于點D，交AC于點G，DF⊥AC于F，交CB的延長線于點E．
（1）求證：直線EF是⊙O的切線；
（2）若sin∠E＝
，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】王老師將
個黑球和若干個白球放入一個不透明的口袋并攪勻，讓若干學生進行摸球實驗，每次摸出一個球（有放回），下表是活動進行中的一組統計數據．
摸球的次數 |
|
|
|
|
|
|
摸到黑球的次數 |
|
|
|
|
|
|
摸到黑球的頻率 |
|
|
|
|
|
補全上表中的有關數據，根據上表數據估計從袋中摸出一個球是黑球的概率是________（精確到0.01）；
估算袋中白球的個數；
在的條件下，若小強同學有放回地連續兩次摸球，用畫樹狀圖或列表的方法計算他兩次都摸出白球的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸，
軸分別交于
，
兩點，點
是 軸上一點，沿直線
折疊
剛好落在 軸上
處．
請解答下列問題：
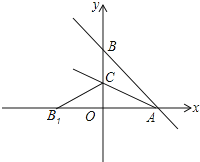
（1），兩點的坐標分別為_____________，____________．
（2）求
的長；
（3）在軸上存在點
，使三角形
為等腰三角形，直接寫出的坐標_____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，A、P、B、C是⊙O上的四點，∠APC=∠CPB=60°，過點C作CM∥BP交PA的延長線于點M．
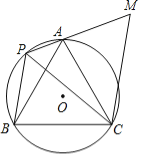
（1）求證：△ACM≌△BCP；
（2）若PA=1，PB=2，求△PCM的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在鈍角三角形
中，
，
，動點
從
點出發到
點止，動點
從
點出發到點止，點運動的速度為
，點運動的速度為
，如果兩點同時開始運動，那么,
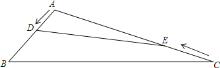
若AD=AE，求
值．
若△ADE和△ABC相似，求的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
