
 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
到2013底,我縣已建立了比較完善的經濟困難學生資助體系.某校2011年發放給每個經濟困難學生450元,2013年發放的金額為625元.設每年發放的資助金額的平均增長率為x,則下面列出的方程中正確的是
A.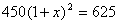 B.
B.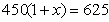
C.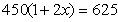 D.
D.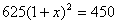
查看答案和解析>>
科目:初中數學 來源: 題型:
閱讀理解:配方法是中學數學的重要方法,用配方法可求最大(小)值。
對于任意正實數a、b,可作如下變形a+b=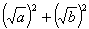 =
=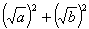 -
- +
+ =
= +
+  ,
,
又∵ ≥0, ∴
≥0, ∴ +
+  ≥0+
≥0+ ,即
,即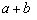 ≥
≥ .
.
(1)根據上述內容,回答下列問題:在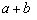 ≥
≥ (a、b均為正實數)中,若ab為定值p,則a+b≥
(a、b均為正實數)中,若ab為定值p,則a+b≥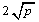 ,當且僅當a、b滿足 時,a+b有最小值
,當且僅當a、b滿足 時,a+b有最小值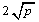 .
.
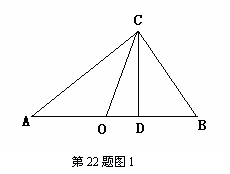
(2)思考驗證:如圖1,△ABC中,∠ACB=90°,CD⊥AB,垂足為D,CO為AB邊上中線,AD=2a,DB=2b, 試根據圖形驗證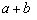 ≥
≥ 成立,并指出等號成立時的條件.
成立,并指出等號成立時的條件.
 (3)探索應用:如圖2,已知A為反比例函數
(3)探索應用:如圖2,已知A為反比例函數 的圖像上一點,A點的橫坐標為1,將一塊三角板的直角頂點放在A處旋轉,保持兩直角邊始終與x軸交于兩點D、E,F(0,-3)為y軸上一點,連結DF、EF,求四邊形ADFE面積的最小值.
的圖像上一點,A點的橫坐標為1,將一塊三角板的直角頂點放在A處旋轉,保持兩直角邊始終與x軸交于兩點D、E,F(0,-3)為y軸上一點,連結DF、EF,求四邊形ADFE面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
小明從家騎車上學,先上坡到達A地后再下坡到達學校,所用的時間與路程如圖所示.如果返回時,上、下坡的速度仍然保持不變,那么他從學校回到家需要的時間是( )
A. 8.6分鐘 B. 9分鐘 C. 12分鐘 D.16分鐘
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,A、M是反比例函數 的圖象上的兩點,過點M作直線MB∥x軸,交
的圖象上的兩點,過點M作直線MB∥x軸,交 軸于點B;過點
軸于點B;過點 作直線
作直線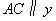 軸交
軸交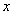 軸于點
軸于點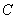 ,交直線MB于點D.BM:DM=8:9,當四邊形OADM的面積為
,交直線MB于點D.BM:DM=8:9,當四邊形OADM的面積為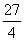 時,k= .
時,k= .
查看答案和解析>>
科目:初中數學 來源: 題型:
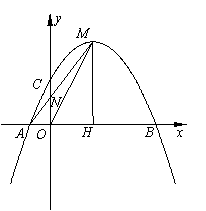
在平面直角坐標系xOy中,已知拋物線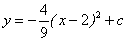 與x軸交于A、B兩點(點A在點B的左側),交y軸的正半軸于點C,其頂點為M,MH⊥x軸于點H,MA交y軸于點N,sin∠MOH=
與x軸交于A、B兩點(點A在點B的左側),交y軸的正半軸于點C,其頂點為M,MH⊥x軸于點H,MA交y軸于點N,sin∠MOH=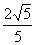 .
.
(1)求此拋物線的函數表達式;
(2)過H的直線與y軸相交于點P,過O,M兩點作直線PH的垂線,垂足分別為E,F,若 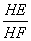 =
=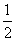 時,求點P的坐標;
時,求點P的坐標;
(3)將(1)中的拋物線沿y軸折疊,使點A落在點D處,連接MD,Q為(1)中的拋物線上的一動點,直線NQ交x軸于點G,當Q點在拋物線上運動時,是否存在點Q,使△ANG 與△ADM相似?若存在,求出所有符合條件的直線QG的解析式;若不存在,請說明理由
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知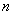 是正整數,則奇數可以用代數式
是正整數,則奇數可以用代數式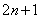 來表示.
來表示.
(1)分解因式: 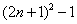 ;
;
(2)我們把所有”奇數的平方減去1”所得的數叫”白銀數”,則所有”白銀數”的最大公約數是多少?請簡要說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com